Школьный 10 - 11 класс

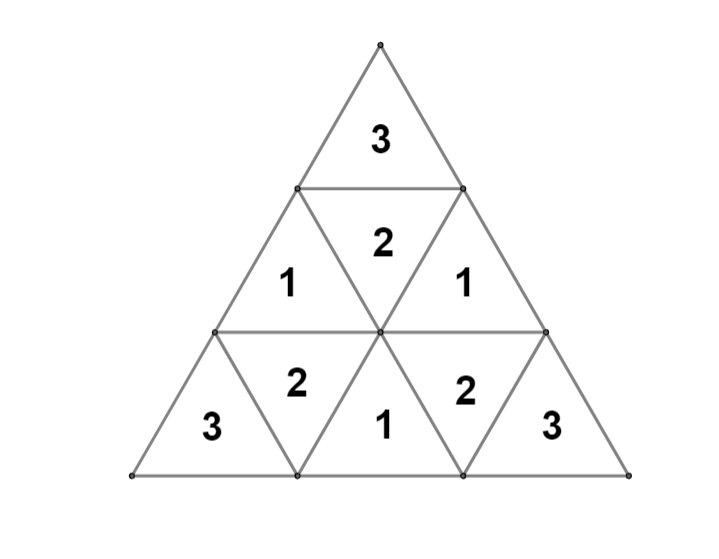
Давайте разобъём треугольники на три группы, которые будем последовательно красить (см. картинку ниже). Общее количество способов покрасить треугольники из первой группы — При этом существует три типа их раскраски, которые мы далее рассмотрим по отдельности: когда они все одинакового цвета, когда они все покрашены в разные цвета, и когда два треугольника покрашены в один цвет, а оставшийся — в третий.

Вариант 1 (треугольники покрашены в один цвет): таких раскрасок ровно три штуки — по одной на каждый цвет. При этом, любой треугольник из второй группы можно покрасить одним из двух способов — ведь оба его соседа покрашены в один и тот же цвет. Итого, способов покрасить треугольники второй группы: . Аналогично, угловые треугольники из третьей группы тоже можно покрасить 8 способами. Итого, раскрасок первого типа: .

Вариант 2 (треугольники покрашены в разные цвета): таких раскрасок шесть штук — вначале нужно выбрать цвет для верхнего треугольника, потом покрасить правый в один из двух оставшихся цветов, и последний треугольник докрасить в оставшийся цвет. Цвет каждого треугольника из второй группы восстанавливается однозначно — ведь у них два соседа разных цветов. Раскрасить же угловые треугольники снова можно 8 способами. Итого, раскрасок второго типа: .

Вариант 3 (два треугольника одного цвета, и третий — другого): это все оставшиеся способы покрасить треугольники из первой группы, а значит, их количество . Теперь у одного треугольника второй группы два одноцветных соседа, а у двух других — два разноцветных соседа. Значит, их можно покрасить способами. С угловыми же треугольниками всё также, как в предыдущих случаях — 8 способов раскраски. Итого, раскрасок третьего типа: .

Наконец, осталось сложить эти три количества и получить ответ: .