Экстремальные задачи в планиметрии
Ошибка.
Попробуйте повторить позже
В выпуклом 12-угольнике все углы равны. Известно, что длины каких-то десяти его сторон равны 1, а длина ещё одной равна 2. Чему может быть равна площадь этого 12-угольника?
Источники:
Подсказка 1
Пусть длины сторон это 10 единиц, 2 и x. Очень хочется найти x... Попробуем рассмотреть векторы, соответствующие сторонам и поработать с ними.
Подсказка 2
Т.к. мы всё-таки хотим использовать длины сторон, то работать будем не с самими векторами, а с коллинеарными им единичными. Т.к. мы знаем, что они образуют многоугольник, то мы можем записать уравнение на них. А как быть с равными углами? Что можно сказать о взаимно расположении некоторых единичных векторов?
Подсказка 3
Заметим, что каждый угол равен 150. Тогда мы можем сказать, какие стороны многоугольника параллельны. Теперь мы можем записать условия на пары единичных векторов.
Подсказка 4
Знаем, что сумма единичных векторов, где один идёт с коэффициентов 2, а другой - с x равна 0. Также сумма единичных векторов, соответствующим противоположным сторонам тоже равна 0. Как найти x?
Подсказка 5
Чему равна сумма единичных векторов без дополнительных коэффициентов?
Подсказка 6
Их сумма равна 0! Теперь-то мы можем найти x) Осталось лишь найти площадь многоугольника, в котором мы знаем взаимное расположение всех сторон.
Рассмотрим 12-угольник удовлетворяющий условию задачи. У него десять сторон длины 1 и одна сторона длины 2.
Обозначим через
длину оставшейся стороны. Рассмотрим векторы
а также коллинеарные им единичные
векторы
Тогда для некоторых
и
имеет место равенство
Помимо того,
поэтому
Вычитая второе из полученных равенств из первого, получаем
Это возможно лишь в случае, если и
Значит, в исходном 12-угольнике есть пара параллельных сторон длины
2.
В силу равенства всех углов и соответствующих сторон этот 12-угольник имеет ось симметрии:
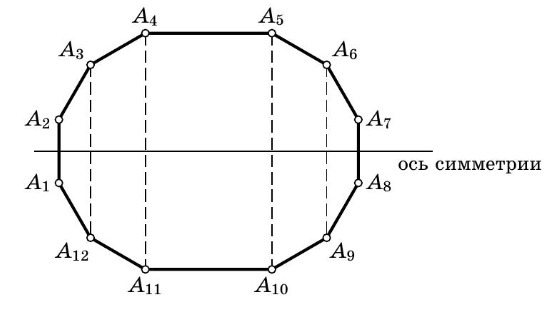
Чтобы найти площадь, разобьём его на 4 трапеции и прямоугольник. Находим
,
поэтому искомая площадь равна
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




