№14 из ЕГЭ 2024
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде стороны основания
равны 12,
а боковые рёбра равны 25. На рёбрах
и
отмечены точки
и
соответственно. Известно, что
a) Докажите, что объём пирамиды составляет
от объёма
пирамиды
б) Найдите площадь сечения пирамиды плоскостью
Источники:
а) Треугольники и
подобны, так как
— общий угол этих
треугольников и
Коэффициент подобия этих треугольников равен Площади
подобных треугольников относятся как квадрат коэффициента подобия, поэтому
получаем
Пусть — высота пирамиды. Опустим из точки
перпендикуляр
на плоскость основания, при этом получим, что точка
лежит на прямой

Треугольники и
подобны, так как
— общий угол этих
треугольников и
Тогда
Тогда
б) Треугольник равнобедренный, поэтому
По теореме косинусов для
Треугольники и
равны, так как
— общая сторона этих
треугольников,
и
так как пирамида правильная.
Тогда
Треугольники и
подобны, поэтому
равносторонний и
Пусть — середина
Тогда
Найдём по теореме Пифагора из
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
точка
— центр основания пирамиды, точка
— середина ребра
точка
делит ребро
в отношении
а
и
а) Докажите, что плоскость параллельна прямой
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) По условию — правильная пирамида, поэтому
— квадрат. Так
как
— центр основания
то
— середина диагонали
Тогда
— средняя линия треугольника
и
Следовательно,
так как прямая
параллельна прямой из этой плоскости.
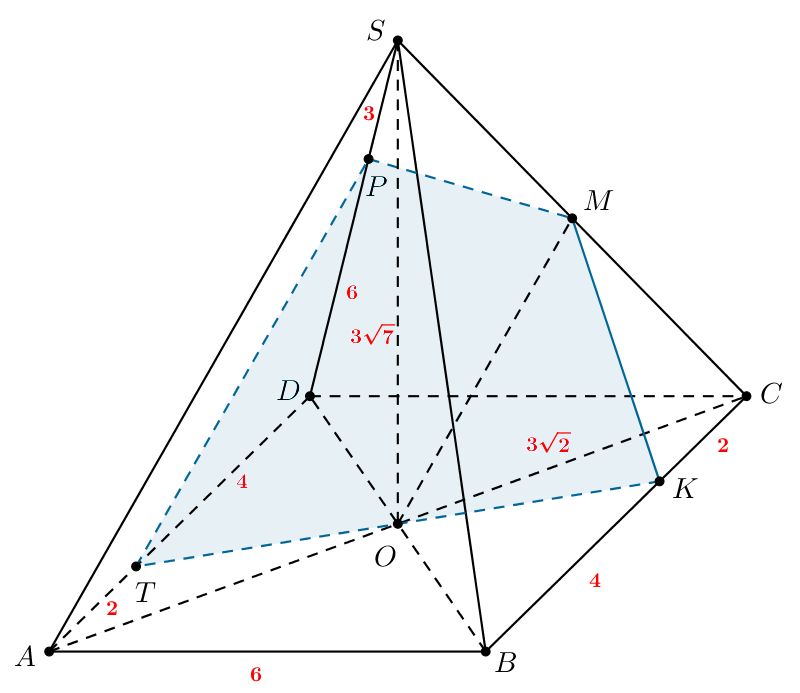
б) Так как — квадрат, то его стороны равны. Тогда
По
условию
поэтому получаем
Пусть прямая пересекает ребро
в точке
Рассмотрим
треугольники
и
В них
так как
— середина
как накрест лежащие углы, образованные параллельными
прямыми
и
и секущей
как вертикальные.
Значит,
по стороне и двум прилежащим к ней углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Значит,
Чтобы построить сечение пирамиды плоскостью через точку
проведём прямую, параллельную
эта прямая будет лежать в
плоскости
Пусть она пересекает ребро
в точке
Тогда
— это сечение пирамиды
плоскостью
и нам
нужно найти отрезок
Диагонали основания
и
равны
поэтому
Мы знаем, что
Найдём боковое ребро
пирамиды по теореме Пифагора из прямоугольного треугольника
Тогда так как — правильная пирамида, то
Так как и
то получаем, что
Заметим, что так как
В треугольнике
известно, что
тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
точка
— центр основания пирамиды, точка
— середина ребра
точка
делит ребро
в отношении
а
и
а) Докажите, что плоскость параллельна прямой
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) По условию — правильная пирамида, поэтому
— квадрат. Так
как
— центр основания
то
— середина диагонали
Тогда
— средняя линия треугольника
и
Следовательно,
так как прямая
параллельна прямой из этой плоскости.
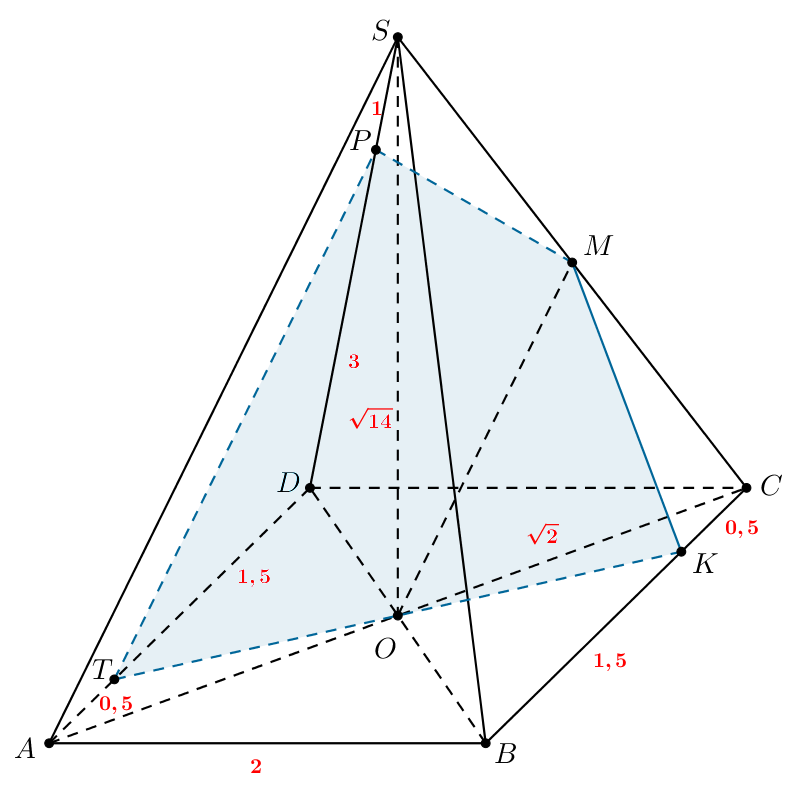
б) Так как — квадрат, то его стороны равны. Тогда
По
условию
поэтому получаем
Пусть прямая пересекает ребро
в точке
Рассмотрим
треугольники
и
В них
так как
— середина
как накрест лежащие углы, образованные параллельными
прямыми
и
и секущей
как вертикальные.
Значит,
по стороне и двум прилежащим к ней углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Значит,
Чтобы построить сечение пирамиды плоскостью через точку
проведём прямую, параллельную
эта прямая будет лежать в плоскости
Пусть она пересекает ребро
в точке
Тогда
— это
сечение пирамиды
плоскостью
и нам нужно найти отрезок
Диагонали основания и
равны
поэтому
Мы знаем,
что
Найдём боковое ребро
пирамиды по теореме Пифагора из
прямоугольного треугольника
Тогда так как — правильная пирамида, то
Так как и
то получаем, что
Заметим, что так как
В треугольнике
известно, что
тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
точка
— центр основания пирамиды, точка
— середина ребра
точка
делит ребро
в отношении
а
и
а) Докажите, что плоскость параллельна прямой
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) По условию — правильная пирамида, поэтому
— квадрат. Так
как
— центр основания
то
— середина диагонали
Тогда
— средняя линия треугольника
и
Следовательно,
так как прямая
параллельна прямой из этой плоскости.

б) Так как — квадрат, то его стороны равны. Тогда
По
условию
поэтому получаем
Пусть прямая пересекает ребро
в точке
Рассмотрим
треугольники
и
В них
так как
— середина
как накрест лежащие углы, образованные параллельными
прямыми
и
и секущей
как вертикальные.
Значит,
по стороне и двум прилежащим к ней углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Значит,
Чтобы построить сечение пирамиды плоскостью через точку
проведём прямую, параллельную
эта прямая будет лежать в плоскости
Пусть она пересекает ребро
в точке
Тогда
— это
сечение пирамиды
плоскостью
и нам нужно найти отрезок
Диагонали основания и
равны
поэтому
Мы
знаем, что
Найдём боковое ребро
пирамиды по теореме
Пифагора из прямоугольного треугольника
Тогда так как — правильная пирамида, то
Так как и
то получаем, что
Заметим, что так как
В треугольнике
известно, что
тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильном тетраэдре точки
и
— середины ребер
и
соответственно.
a) Докажите, что прямая перпендикулярна ребрам
и
б) Плоскость перпендикулярна прямой
и пересекает ребро
в
точке
Найдите площадь сечения тетраэдра
плоскостью
если
известно, что
Источники:
а) Так как тетраэдр правильный, то все его ребра равны и все грани являются
равными правильными треугольниками. Так как и
— медианы в равных
правильных треугольниках
и
то
Тогда
равнобедренный, следовательно, медиана
проведенная к основанию, также
является и высотой. Таким образом,
Аналогично
равнобедренный и
— медиана и высота этого треугольника, то есть

б) Если то
проходит через прямые, параллельные
и
то есть
Тогда
пересекает плоскость
по
прямой
а плоскости
и
по прямым
и
соответственно, параллельным
Тогда
— сечение тетраэдра
плоскостью
Далее имеем и
так как
и
— медианы в
равносторонних треугольниках. Тогда
следовательно,
Значит,
— прямоугольник.
Треугольники и
подобны, так как
откуда
Треугольники и
подобны, так как
откуда
Следовательно, площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильном тетраэдре точки
и
— середины ребер
и
соответственно. Плоскость
перпендикулярна прямой
и пересекает ребро
в точке
a) Докажите, что прямая перпендикулярна ребрам
и
б) Найдите площадь сечения тетраэдра плоскостью
если известно,
что
Источники:
а) Так как тетраэдр правильный, то все его ребра равны и все грани являются
равными правильными треугольниками. Так как и
— медианы в равных
правильных треугольниках
и
то
Тогда
равнобедренный, следовательно, медиана
проведенная к основанию, также
является и высотой. Таким образом,
Аналогично
равнобедренный и
— медиана и высота этого треугольника, то есть

б) Если то
проходит через прямые, параллельные
и
то есть
Тогда
пересекает плоскость
по
прямой
а плоскости
и
по прямым
и
соответственно, параллельным
Тогда
— сечение тетраэдра
плоскостью
Далее имеем и
так как
и
— медианы в
равносторонних треугольниках. Тогда
следовательно,
Значит,
— прямоугольник.
Треугольники и
подобны, так как
откуда
Треугольники и
подобны, так как
откуда
Следовательно, площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде точка
— центр основания
Точка
делит ребро
в отношении
Плоскость
проходящая через точки
и
и параллельная ребру
пересекает
ребро
в точке
Известно, что
а) Докажите, что точка — середина
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) В правильной четырехугольной пирамиде основание является
квадратом, тогда
— точка пересечения его диагоналей
и
значит,
— середина
и
Плоскость пересекает плоскость
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Таким образом,
Следовательно,
— средняя
линия треугольника
так как
и
— середина
Значит,
— середина

б) Плоскость пересекает плоскость грани
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Пусть — точка пересечения плоскости
и ребра
Тогда
Следовательно, по теореме о пропорциональных отрезках
По условию — правильная пирамида,
Значит, все
ребра пирамиды равны 6. Тогда
Плоскость проходит через точки
и
следовательно, пересекает
плоскость основания
по прямой
Пусть
пересекает
в точке

Рассмотрим и
В них
так как
—
середина
как накрест лежащие углы, образованные
параллельными прямыми
и
и секущей
как
вертикальные. Значит,
по стороне и двум прилежащим к ней
углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Так как по условию точка — середина отрезка
и
то
Нам нужно найти длину отрезка так как по нему плоскость
пересекает грань
Все ребра пирамиды равны, поэтому — равносторонний. Тогда
По теореме косинусов для
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде точка
— центр основания
Точка
делит ребро
в отношении
Плоскость
проходящая через точки
и
и параллельная ребру
пересекает
ребро
в точке
Известно, что
а) Докажите, что точка — середина
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) В правильной четырехугольной пирамиде основание является
квадратом, тогда
— точка пересечения его диагоналей
и
значит,
— середина
и
Плоскость пересекает плоскость
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Таким образом,
Следовательно,
— средняя
линия треугольника
так как
и
— середина
Значит,
— середина
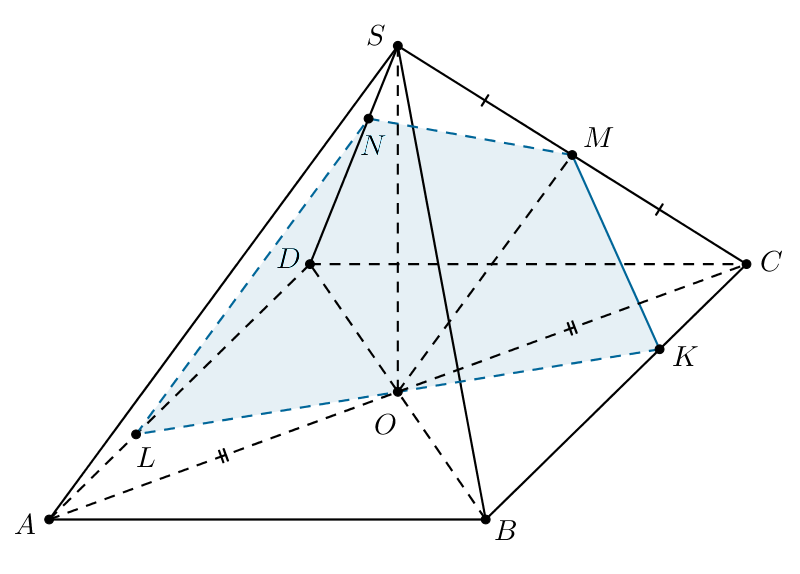
б) Плоскость пересекает плоскость грани
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Пусть — точка пересечения плоскости
и ребра
Тогда
Следовательно, по теореме о пропорциональных отрезках
По условию — правильная пирамида,
Значит, все
ребра пирамиды равны 10. Тогда
Плоскость проходит через точки
и
следовательно, пересекает
плоскость основания
по прямой
Пусть
пересекает
в точке
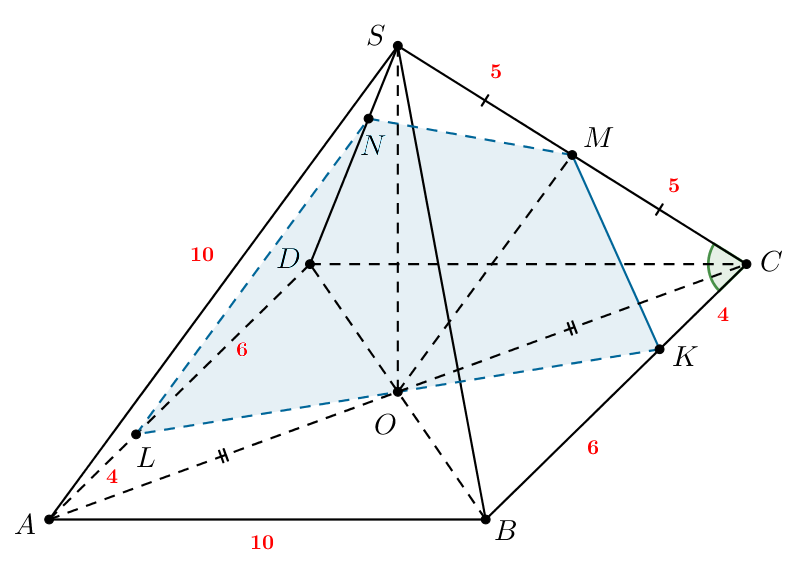
Рассмотрим и
В них
так как
—
середина
как накрест лежащие углы, образованные
параллельными прямыми
и
и секущей
как
вертикальные. Значит,
по стороне и двум прилежащим к ней
углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Так как по условию точка — середина отрезка
и
то
Нам нужно найти длину отрезка так как по нему плоскость
пересекает грань
Все ребра пирамиды равны, поэтому — равносторонний. Тогда
По теореме косинусов для
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде точка
— центр основания
Точка
делит ребро
в отношении
Плоскость
проходящая через точки
и
и параллельная ребру
пересекает
ребро
в точке
Известно, что
а) Докажите, что точка — середина
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) В правильной четырехугольной пирамиде основание является
квадратом, тогда
— точка пересечения его диагоналей
и
значит,
— середина
и
Плоскость пересекает плоскость
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Таким образом,
Следовательно,
— средняя
линия треугольника
так как
и
— середина
Значит,
— середина
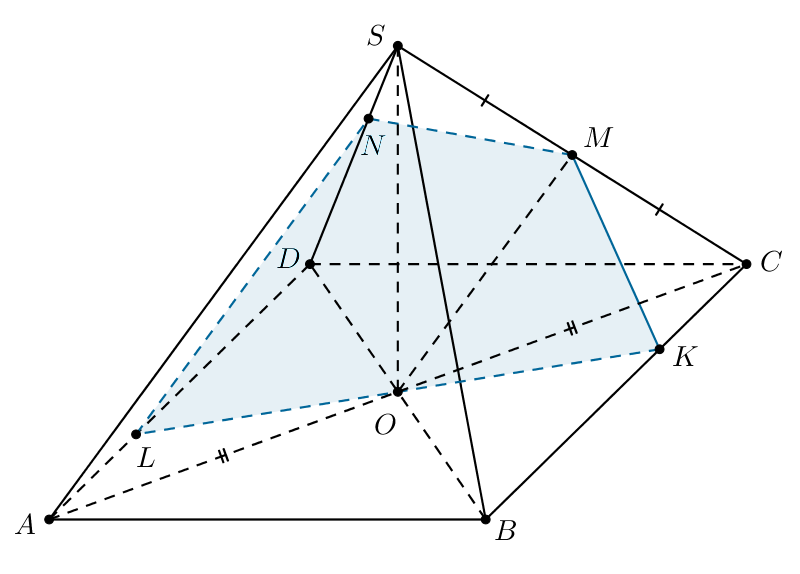
б) Плоскость пересекает плоскость грани
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Пусть — точка пересечения плоскости
и ребра
Тогда
Следовательно, по теореме о пропорциональных отрезках
По условию — правильная пирамида,
Значит, все
ребра пирамиды равны 4. Тогда
Плоскость проходит через точки
и
следовательно, пересекает
плоскость основания
по прямой
Пусть
пересекает
в точке

Рассмотрим и
В них
так как
—
середина
как накрест лежащие углы, образованные
параллельными прямыми
и
и секущей
как
вертикальные. Значит,
по стороне и двум прилежащим к ней
углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Так как по условию точка — середина отрезка
и
то
Нам нужно найти длину отрезка так как по нему плоскость
пересекает грань
Все ребра пирамиды равны, поэтому — равносторонний. Тогда
По теореме косинусов для
б)
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде с основанием
точки
и
— середины ребер
и
соответственно. На продолжении ребра
за
точку
отмечена точка
Прямые
и
пересекают ребра
и
в точках
и
соответственно, причем
a) Докажите, что прямые и
пересекаются.
б) Найдите отношение
Источники:
а) Рассмотрим плоскость Точка
лежит на прямой
поэтому
лежит и в плоскости
Точка
лежит на прямой
поэтому лежит и
в плоскости
Значит, прямые
и
лежат в плоскости
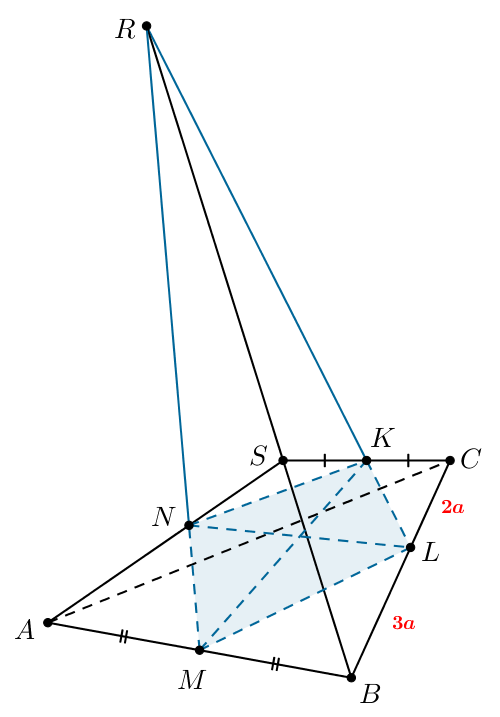
— четырехугольник, а
и
— его диагонали, следовательно,
прямые, содержащие их, пересекаются.
б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная пирамида точки
и
— середины рёбер
и
соответственно. Точки
и
на ребрах
и
соответственно
расположены таким образом, что
и прямые
и
пересекаются.
а) Докажите, что прямые
и
пересекаются в одной
точке.
б) Найдите отношение
Источники:
а) Так как прямые и
пересекаются, то точки
лежат в
одной плоскости. Тогда плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
Если три плоскости
попарно пересекаются по трём прямым, то либо эти прямые параллельны
друг другу, либо это одна и та же прямая, либо они пересекаются в одной
точке.
Параллельными эти прямые быть не могут, иначе получаем и
так как
— это середина
то
будет средней линией треугольника
Но по условию точка
не является серединой
Противоречие.
Совпадать эти прямые тоже не могут, так как прямые и
лежат в
плоскостях разных граней. Значит, прямые
и
пересекаются в
одной точке.

б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная пирамида точки
и
— середины рёбер
и
соответственно. Точки
и
на ребрах
и
соответственно
расположены таким образом, что
и прямые
и
пересекаются.
а) Докажите, что прямые
и
пересекаются в одной
точке.
б) Найдите отношение
Источники:
а) Так как прямые и
пересекаются, то точки
лежат в
одной плоскости. Тогда плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
Если три плоскости
попарно пересекаются по трём прямым, то либо эти прямые параллельны
друг другу, либо это одна и та же прямая, либо они пересекаются в одной
точке.
Параллельными эти прямые быть не могут, иначе получаем и
так как
— это середина
то
будет средней линией треугольника
Но по условию точка
не является серединой
Противоречие.
Совпадать эти прямые тоже не могут, так как прямые и
лежат в
плоскостях разных граней. Значит, прямые
и
пересекаются в
одной точке.

б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная пирамида точки
и
— середины рёбер
и
соответственно. Точки
и
на ребрах
и
соответственно
расположены таким образом, что
и прямые
и
пересекаются.
а) Докажите, что прямые
и
пересекаются в одной
точке.
б) Найдите отношение
Источники:
а) Так как прямые и
пересекаются, то точки
лежат в
одной плоскости. Тогда плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
Если три плоскости
попарно пересекаются по трём прямым, то либо эти прямые параллельны
друг другу, либо это одна и та же прямая, либо они пересекаются в одной
точке.
Параллельными эти прямые быть не могут, иначе получаем и
так как
— это середина
то
будет средней линией треугольника
Но по условию точка
не является серединой
Противоречие.
Совпадать эти прямые тоже не могут, так как прямые и
лежат в
плоскостях разных граней. Значит, прямые
и
пересекаются в
одной точке.

б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,
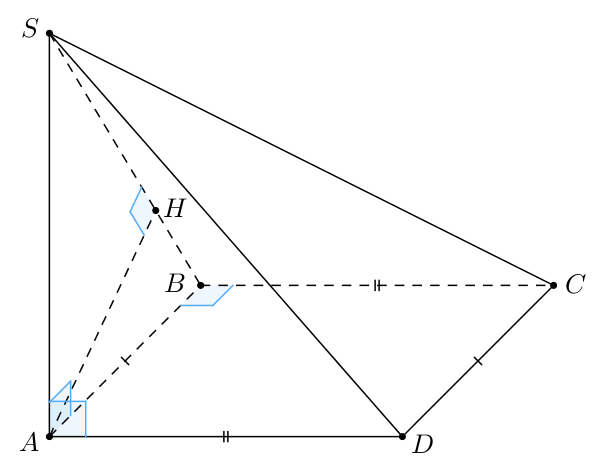
б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,
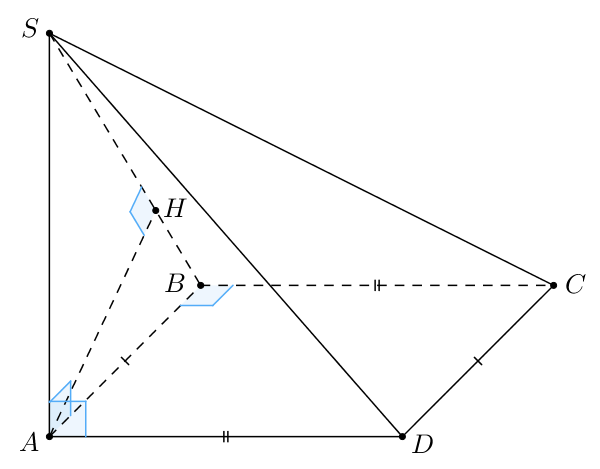
б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,

б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,
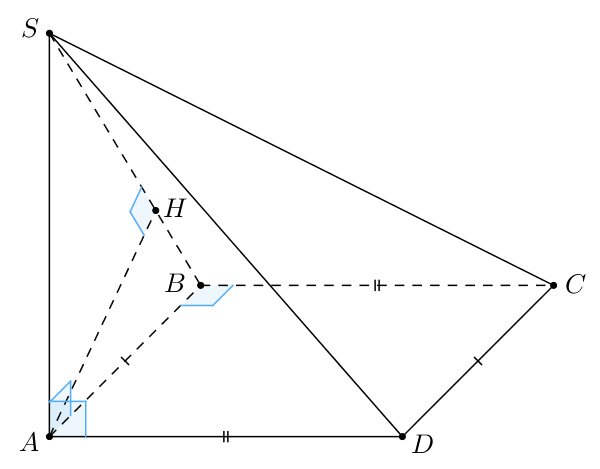
б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите угол между прямыми и
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,

б) По теореме Пифагора для прямоугольного треугольника
Тогда Пусть
— середина
— середина
Тогда
По предыдущему пункту значит,
Тогда по теореме
Пифагора для треугольника
Заметим, что — средняя линия треугольника
значит,
и
Тогда угол между прямыми и
равен углу между прямыми
и
По теореме Пифагора для треугольника
Значит, по теореме косинусов для треугольника
Так как то
Значит, угол между прямыми
и
равен углу
Тогда и угол между прямыми
и
равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите угол между прямыми и
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,

б) По теореме Пифагора для прямоугольного треугольника
Тогда Пусть
— середина
— середина
Тогда
По предыдущему пункту значит,
Тогда по теореме
Пифагора для треугольника
Заметим, что — средняя линия треугольника
значит,
и
Тогда угол между прямыми и
равен углу между прямыми
и
По теореме Пифагора для треугольника
Значит, по теореме косинусов для треугольника
Так как то
Значит, угол между прямыми
и
равен углу, смежному
Тогда и угол между прямыми
и
равен
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите угол между прямыми и
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,

б) По теореме Пифагора для прямоугольного треугольника
Тогда Пусть
— середина
— середина
Тогда
По предыдущему пункту значит,
Тогда по теореме
Пифагора для треугольника
Заметим, что — средняя линия треугольника
значит,
и
Тогда угол между прямыми и
равен углу между прямыми
и
По теореме Пифагора для треугольника
Значит, по теореме косинусов для треугольника
Так как то
Значит, угол между прямыми
и
равен углу, смежному
Тогда и угол между прямыми
и
равен
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



