19.22 Оценка + пример
Ошибка.
Попробуйте повторить позже
Какое наименьшее число клеточек на доске можно закрасить в черный цвет так, чтобы была хотя
бы одна закрашенная клетка
а) в любом квадратике
б) в любом уголке из трёх клеточек?
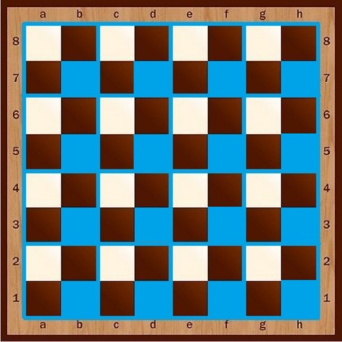
а) Разобьем шахматную доску на клеток
как показано на рисунке

Так как всего квадратов 16 штук, то минимальное количество закрашенных клеток 16 (так
как если мы закрасим всего 15 клеток, то в каком то из 16 квадратов
не будет закрашенной
клетки).
Это была оценка, то есть доказательство того, что меньше 16 клеток закрасить мы не сможем.
Пример того, как это можно сделать ниже:
б) Воспользуемся разбиением шахматной доски из пункта а).
Заметим, что если в каком-то из 16 квадратов будет закрашена только 1 клетка, то в этом квадрате
обязательно будет уголок из трех клеточек, в котором не будет закрашенной клетки. Поэтому в
каждом из 16 квадратов
должно быть как минимум 2 закрашенные клетки, то есть всего 32
закрашенные клетки.
Это была оценка, то есть доказательство того, что меньше чем 32 клетки закрасить нам не удастся.
Пример для 32 на рисунке ниже:

a) 16
б) 32.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




