14.01 Задачи №14 из ЕГЭ прошлых лет
Ошибка.
Попробуйте повторить позже
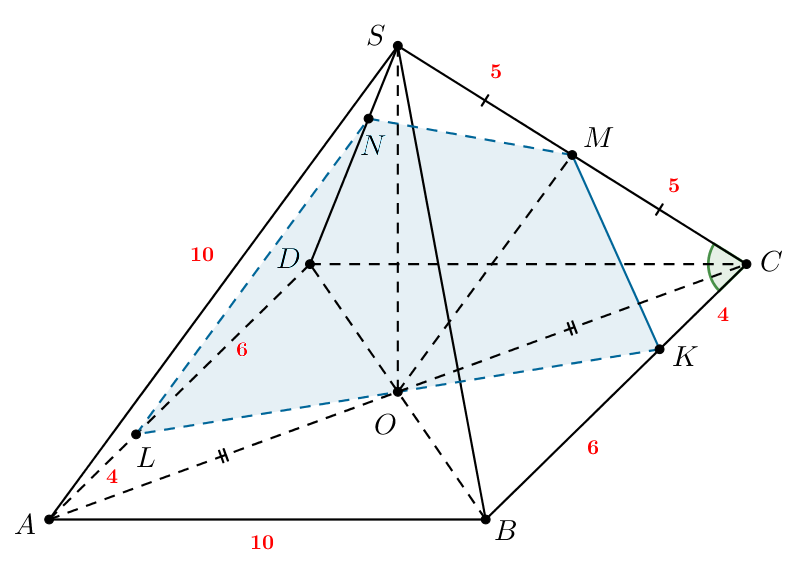
Дана правильная треугольная пирамида сторона основания
высота
точка
— середина
Плоскость, проходящая через точку
и параллельная основанию пирамиды, пересекает ребра
и
в точках
и
соответственно.
а) Докажите, что площадь относится к площади
как
б) Найдите объем пирамиды
Источники:
а) Обозначим плоскость через
По условию плоскости
и
параллельны, следовательно, они пересекают
плоскость
по параллельным прямым. Плоскость
пересекает плоскость
по прямой
плоскость
пересекает плоскость
по прямой
Тогда получаем, что
По аналогичным соображениям
Далее, причем
— середина
следовательно,
— средняя линия в треугольнике
и точка
—
середина
Аналогично получаем, что точка
— середина
Тогда
— средняя линия треугольника
параллельная стороне
Следовательно,
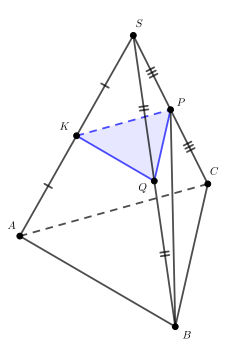
Обозначим через длину высоты треугольника
проведенной из вершины
Так как
— средняя линия, то она
делит эту высоту пополам. Следовательно, высота трапеции
равна
Теперь можем найти отношение площади
к площади
б) Расписав объем пирамиды через объемы ее составных частей, получим
Найдем все эти объемы, чтобы затем найти объем пирамиды
Площадь правильного треугольника со стороной
равна

Высота пирамиды
равна 10, тогда ее объем равен
Далее, найдем следующие отрезки как средние линии соответствующих треугольников:
Следовательно, треугольник подобен треугольнику
по трем сторонам с коэффициентом
Тогда
получаем
Пусть — точка пересечения
с плоскостью
Далее,
следовательно,
— высота пирамиды
Так как
и
— прямые пересечения плоскости
с параллельными плоскостями
и
то они
параллельны. Тогда в треугольнике
отрезок
проходит через середину
и параллелен
Значит,
—
средняя линия и

Тогда можем найти объем пирамиды
Высота из вершины пирамиды
равна
так как
а
и есть расстояние между этими
плоскостями. Тогда можем найти объем пирамиды
Осталось вычислить объем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
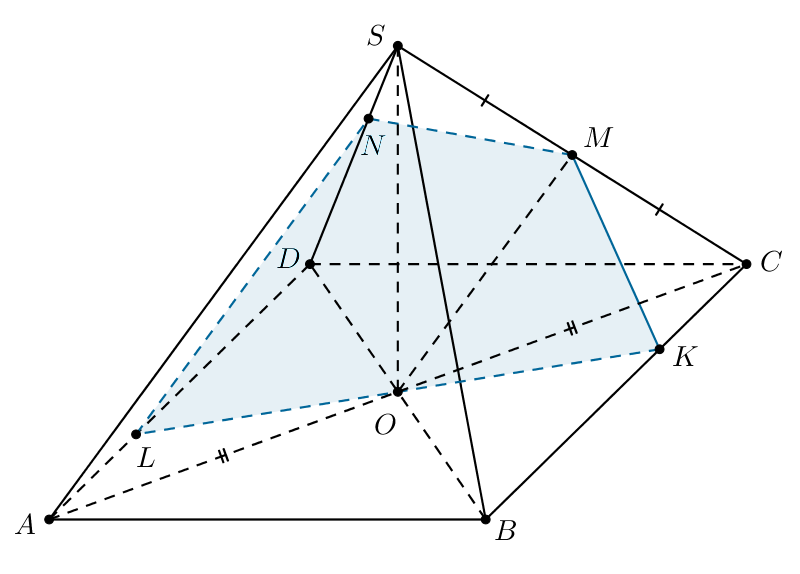
В правильной треугольной пирамиде стороны основания
равны 12,
а боковые рёбра равны 25. На рёбрах
и
отмечены точки
и
соответственно. Известно, что
a) Докажите, что объём пирамиды составляет
от объёма
пирамиды
б) Найдите площадь сечения пирамиды плоскостью
Источники:
а) Треугольники и
подобны, так как
— общий угол этих
треугольников и
Коэффициент подобия этих треугольников равен Площади
подобных треугольников относятся как квадрат коэффициента подобия, поэтому
получаем
Пусть — высота пирамиды. Опустим из точки
перпендикуляр
на плоскость основания, при этом получим, что точка
лежит на прямой

Треугольники и
подобны, так как
— общий угол этих
треугольников и
Тогда
Тогда
б) Треугольник равнобедренный, поэтому
По теореме косинусов для
Треугольники и
равны, так как
— общая сторона этих
треугольников,
и
так как пирамида правильная.
Тогда
Треугольники и
подобны, поэтому
равносторонний и
Пусть — середина
Тогда
Найдём по теореме Пифагора из
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
точка
— центр основания пирамиды, точка
— середина ребра
точка
делит ребро
в отношении
а
и
а) Докажите, что плоскость параллельна прямой
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) По условию — правильная пирамида, поэтому
— квадрат. Так
как
— центр основания
то
— середина диагонали
Тогда
— средняя линия треугольника
и
Следовательно,
так как прямая
параллельна прямой из этой плоскости.
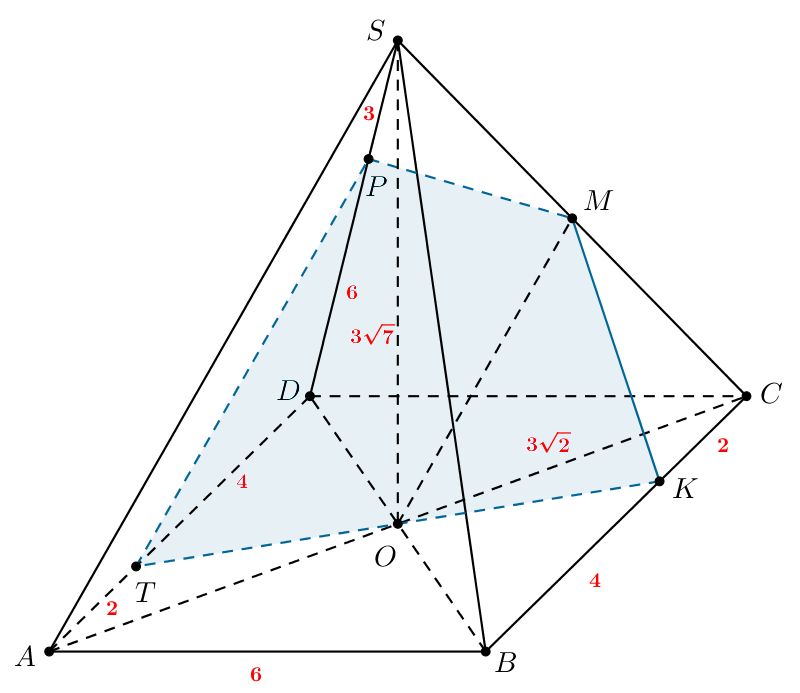
б) Так как — квадрат, то его стороны равны. Тогда
По
условию
поэтому получаем
Пусть прямая пересекает ребро
в точке
Рассмотрим
треугольники
и
В них
так как
— середина
как накрест лежащие углы, образованные параллельными
прямыми
и
и секущей
как вертикальные.
Значит,
по стороне и двум прилежащим к ней углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Значит,
Чтобы построить сечение пирамиды плоскостью через точку
проведём прямую, параллельную
эта прямая будет лежать в
плоскости
Пусть она пересекает ребро
в точке
Тогда
— это сечение пирамиды
плоскостью
и нам
нужно найти отрезок
Диагонали основания
и
равны
поэтому
Мы знаем, что
Найдём боковое ребро
пирамиды по теореме Пифагора из прямоугольного треугольника
Тогда так как — правильная пирамида, то
Так как и
то получаем, что
Заметим, что так как
В треугольнике
известно, что
тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
точка
— центр основания пирамиды, точка
— середина ребра
точка
делит ребро
в отношении
а
и
а) Докажите, что плоскость параллельна прямой
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) По условию — правильная пирамида, поэтому
— квадрат. Так
как
— центр основания
то
— середина диагонали
Тогда
— средняя линия треугольника
и
Следовательно,
так как прямая
параллельна прямой из этой плоскости.
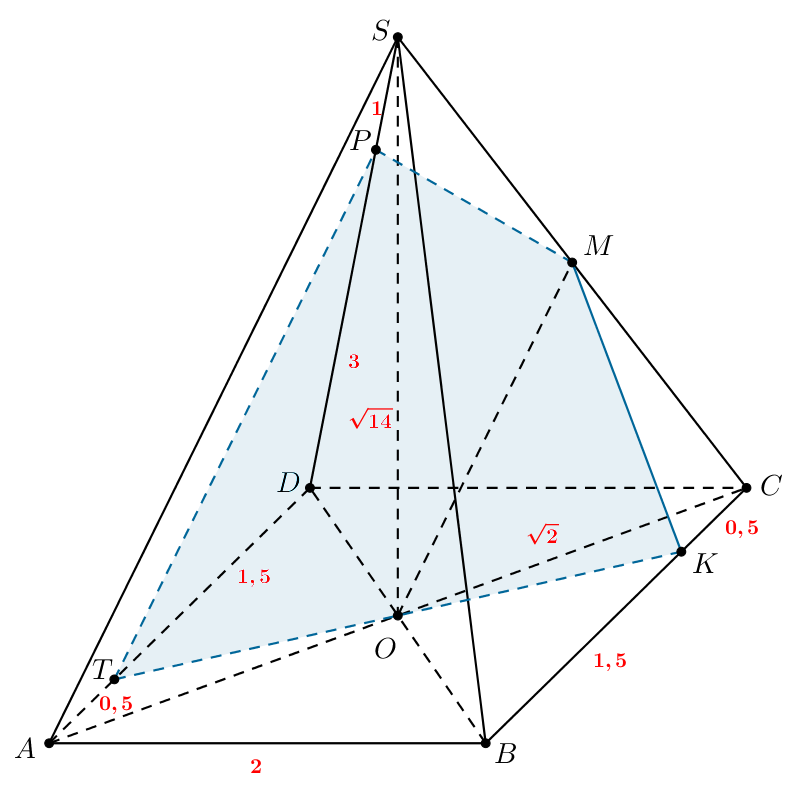
б) Так как — квадрат, то его стороны равны. Тогда
По
условию
поэтому получаем
Пусть прямая пересекает ребро
в точке
Рассмотрим
треугольники
и
В них
так как
— середина
как накрест лежащие углы, образованные параллельными
прямыми
и
и секущей
как вертикальные.
Значит,
по стороне и двум прилежащим к ней углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Значит,
Чтобы построить сечение пирамиды плоскостью через точку
проведём прямую, параллельную
эта прямая будет лежать в плоскости
Пусть она пересекает ребро
в точке
Тогда
— это
сечение пирамиды
плоскостью
и нам нужно найти отрезок
Диагонали основания и
равны
поэтому
Мы знаем,
что
Найдём боковое ребро
пирамиды по теореме Пифагора из
прямоугольного треугольника
Тогда так как — правильная пирамида, то
Так как и
то получаем, что
Заметим, что так как
В треугольнике
известно, что
тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
точка
— центр основания пирамиды, точка
— середина ребра
точка
делит ребро
в отношении
а
и
а) Докажите, что плоскость параллельна прямой
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) По условию — правильная пирамида, поэтому
— квадрат. Так
как
— центр основания
то
— середина диагонали
Тогда
— средняя линия треугольника
и
Следовательно,
так как прямая
параллельна прямой из этой плоскости.

б) Так как — квадрат, то его стороны равны. Тогда
По
условию
поэтому получаем
Пусть прямая пересекает ребро
в точке
Рассмотрим
треугольники
и
В них
так как
— середина
как накрест лежащие углы, образованные параллельными
прямыми
и
и секущей
как вертикальные.
Значит,
по стороне и двум прилежащим к ней углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Значит,
Чтобы построить сечение пирамиды плоскостью через точку
проведём прямую, параллельную
эта прямая будет лежать в плоскости
Пусть она пересекает ребро
в точке
Тогда
— это
сечение пирамиды
плоскостью
и нам нужно найти отрезок
Диагонали основания и
равны
поэтому
Мы
знаем, что
Найдём боковое ребро
пирамиды по теореме
Пифагора из прямоугольного треугольника
Тогда так как — правильная пирамида, то
Так как и
то получаем, что
Заметим, что так как
В треугольнике
известно, что
тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильном тетраэдре точки
и
— середины ребер
и
соответственно.
a) Докажите, что прямая перпендикулярна ребрам
и
б) Плоскость перпендикулярна прямой
и пересекает ребро
в
точке
Найдите площадь сечения тетраэдра
плоскостью
если
известно, что
Источники:
а) Так как тетраэдр правильный, то все его ребра равны и все грани являются
равными правильными треугольниками. Так как и
— медианы в равных
правильных треугольниках
и
то
Тогда
равнобедренный, следовательно, медиана
проведенная к основанию, также
является и высотой. Таким образом,
Аналогично
равнобедренный и
— медиана и высота этого треугольника, то есть

б) Если то
проходит через прямые, параллельные
и
то есть
Тогда
пересекает плоскость
по
прямой
а плоскости
и
по прямым
и
соответственно, параллельным
Тогда
— сечение тетраэдра
плоскостью
Далее имеем и
так как
и
— медианы в
равносторонних треугольниках. Тогда
следовательно,
Значит,
— прямоугольник.
Треугольники и
подобны, так как
откуда
Треугольники и
подобны, так как
откуда
Следовательно, площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильном тетраэдре точки
и
— середины ребер
и
соответственно. Плоскость
перпендикулярна прямой
и пересекает ребро
в точке
a) Докажите, что прямая перпендикулярна ребрам
и
б) Найдите площадь сечения тетраэдра плоскостью
если известно,
что
Источники:
а) Так как тетраэдр правильный, то все его ребра равны и все грани являются
равными правильными треугольниками. Так как и
— медианы в равных
правильных треугольниках
и
то
Тогда
равнобедренный, следовательно, медиана
проведенная к основанию, также
является и высотой. Таким образом,
Аналогично
равнобедренный и
— медиана и высота этого треугольника, то есть

б) Если то
проходит через прямые, параллельные
и
то есть
Тогда
пересекает плоскость
по
прямой
а плоскости
и
по прямым
и
соответственно, параллельным
Тогда
— сечение тетраэдра
плоскостью
Далее имеем и
так как
и
— медианы в
равносторонних треугольниках. Тогда
следовательно,
Значит,
— прямоугольник.
Треугольники и
подобны, так как
откуда
Треугольники и
подобны, так как
откуда
Следовательно, площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде точка
— центр основания
Точка
делит ребро
в отношении
Плоскость
проходящая через точки
и
и параллельная ребру
пересекает
ребро
в точке
Известно, что
а) Докажите, что точка — середина
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) В правильной четырехугольной пирамиде основание является
квадратом, тогда
— точка пересечения его диагоналей
и
значит,
— середина
и
Плоскость пересекает плоскость
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Таким образом,
Следовательно,
— средняя
линия треугольника
так как
и
— середина
Значит,
— середина

б) Плоскость пересекает плоскость грани
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Пусть — точка пересечения плоскости
и ребра
Тогда
Следовательно, по теореме о пропорциональных отрезках
По условию — правильная пирамида,
Значит, все
ребра пирамиды равны 6. Тогда
Плоскость проходит через точки
и
следовательно, пересекает
плоскость основания
по прямой
Пусть
пересекает
в точке

Рассмотрим и
В них
так как
—
середина
как накрест лежащие углы, образованные
параллельными прямыми
и
и секущей
как
вертикальные. Значит,
по стороне и двум прилежащим к ней
углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Так как по условию точка — середина отрезка
и
то
Нам нужно найти длину отрезка так как по нему плоскость
пересекает грань
Все ребра пирамиды равны, поэтому — равносторонний. Тогда
По теореме косинусов для
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде точка
— центр основания
Точка
делит ребро
в отношении
Плоскость
проходящая через точки
и
и параллельная ребру
пересекает
ребро
в точке
Известно, что
а) Докажите, что точка — середина
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) В правильной четырехугольной пирамиде основание является
квадратом, тогда
— точка пересечения его диагоналей
и
значит,
— середина
и
Плоскость пересекает плоскость
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Таким образом,
Следовательно,
— средняя
линия треугольника
так как
и
— середина
Значит,
— середина
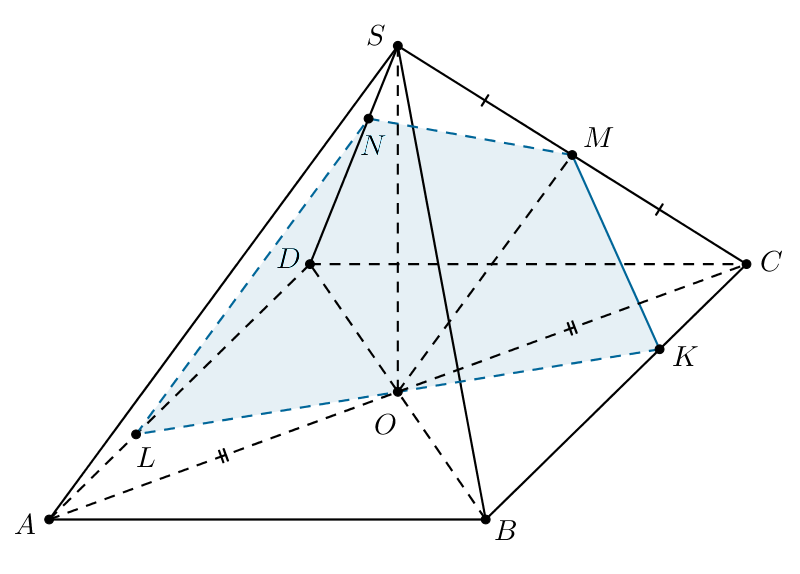
б) Плоскость пересекает плоскость грани
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Пусть — точка пересечения плоскости
и ребра
Тогда
Следовательно, по теореме о пропорциональных отрезках
По условию — правильная пирамида,
Значит, все
ребра пирамиды равны 10. Тогда
Плоскость проходит через точки
и
следовательно, пересекает
плоскость основания
по прямой
Пусть
пересекает
в точке
Рассмотрим и
В них
так как
—
середина
как накрест лежащие углы, образованные
параллельными прямыми
и
и секущей
как
вертикальные. Значит,
по стороне и двум прилежащим к ней
углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Так как по условию точка — середина отрезка
и
то
Нам нужно найти длину отрезка так как по нему плоскость
пересекает грань
Все ребра пирамиды равны, поэтому — равносторонний. Тогда
По теореме косинусов для
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде точка
— центр основания
Точка
делит ребро
в отношении
Плоскость
проходящая через точки
и
и параллельная ребру
пересекает
ребро
в точке
Известно, что
а) Докажите, что точка — середина
б) Найдите длину отрезка, по которому плоскость пересечёт грань
Источники:
а) В правильной четырехугольной пирамиде основание является
квадратом, тогда
— точка пересечения его диагоналей
и
значит,
— середина
и
Плоскость пересекает плоскость
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Таким образом,
Следовательно,
— средняя
линия треугольника
так как
и
— середина
Значит,
— середина
б) Плоскость пересекает плоскость грани
и параллельна прямой
лежащей в этой плоскости. Значит, плоскость
пересекает
по прямой,
параллельной
Пусть — точка пересечения плоскости
и ребра
Тогда
Следовательно, по теореме о пропорциональных отрезках
По условию — правильная пирамида,
Значит, все
ребра пирамиды равны 4. Тогда
Плоскость проходит через точки
и
следовательно, пересекает
плоскость основания
по прямой
Пусть
пересекает
в точке

Рассмотрим и
В них
так как
—
середина
как накрест лежащие углы, образованные
параллельными прямыми
и
и секущей
как
вертикальные. Значит,
по стороне и двум прилежащим к ней
углам.
В равных треугольниках соответствующие элементы равны, поэтому
Тогда
Так как по условию точка — середина отрезка
и
то
Нам нужно найти длину отрезка так как по нему плоскость
пересекает грань
Все ребра пирамиды равны, поэтому — равносторонний. Тогда
По теореме косинусов для
б)
Ошибка.
Попробуйте повторить позже
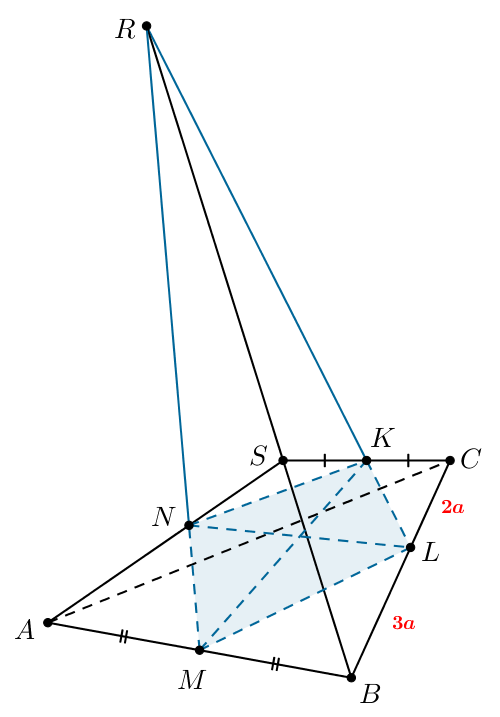
В правильной треугольной пирамиде с основанием
точки
и
— середины ребер
и
соответственно. На продолжении ребра
за
точку
отмечена точка
Прямые
и
пересекают ребра
и
в точках
и
соответственно, причем
a) Докажите, что прямые и
пересекаются.
б) Найдите отношение
Источники:
а) Рассмотрим плоскость Точка
лежит на прямой
поэтому
лежит и в плоскости
Точка
лежит на прямой
поэтому лежит и
в плоскости
Значит, прямые
и
лежат в плоскости
— четырехугольник, а
и
— его диагонали, следовательно,
прямые, содержащие их, пересекаются.
б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная пирамида точки
и
— середины рёбер
и
соответственно. Точки
и
на ребрах
и
соответственно
расположены таким образом, что
и прямые
и
пересекаются.
а) Докажите, что прямые
и
пересекаются в одной
точке.
б) Найдите отношение
Источники:
а) Так как прямые и
пересекаются, то точки
лежат в
одной плоскости. Тогда плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
Если три плоскости
попарно пересекаются по трём прямым, то либо эти прямые параллельны
друг другу, либо это одна и та же прямая, либо они пересекаются в одной
точке.
Параллельными эти прямые быть не могут, иначе получаем и
так как
— это середина
то
будет средней линией треугольника
Но по условию точка
не является серединой
Противоречие.
Совпадать эти прямые тоже не могут, так как прямые и
лежат в
плоскостях разных граней. Значит, прямые
и
пересекаются в
одной точке.

б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная пирамида точки
и
— середины рёбер
и
соответственно. Точки
и
на ребрах
и
соответственно
расположены таким образом, что
и прямые
и
пересекаются.
а) Докажите, что прямые
и
пересекаются в одной
точке.
б) Найдите отношение
Источники:
а) Так как прямые и
пересекаются, то точки
лежат в
одной плоскости. Тогда плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
Если три плоскости
попарно пересекаются по трём прямым, то либо эти прямые параллельны
друг другу, либо это одна и та же прямая, либо они пересекаются в одной
точке.
Параллельными эти прямые быть не могут, иначе получаем и
так как
— это середина
то
будет средней линией треугольника
Но по условию точка
не является серединой
Противоречие.
Совпадать эти прямые тоже не могут, так как прямые и
лежат в
плоскостях разных граней. Значит, прямые
и
пересекаются в
одной точке.

б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная пирамида точки
и
— середины рёбер
и
соответственно. Точки
и
на ребрах
и
соответственно
расположены таким образом, что
и прямые
и
пересекаются.
а) Докажите, что прямые
и
пересекаются в одной
точке.
б) Найдите отношение
Источники:
а) Так как прямые и
пересекаются, то точки
лежат в
одной плоскости. Тогда плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
плоскости
и
пересекаются по прямой
Если три плоскости
попарно пересекаются по трём прямым, то либо эти прямые параллельны
друг другу, либо это одна и та же прямая, либо они пересекаются в одной
точке.
Параллельными эти прямые быть не могут, иначе получаем и
так как
— это середина
то
будет средней линией треугольника
Но по условию точка
не является серединой
Противоречие.
Совпадать эти прямые тоже не могут, так как прямые и
лежат в
плоскостях разных граней. Значит, прямые
и
пересекаются в
одной точке.

б) По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме отмечены середины
и
ребер
и
соответственно.
а) Докажите, что плоскость делит отрезок
в отношении 2:3,
считая от вершины
б) Найдите объем пирамиды если сторона основания призмы равна
6, а боковое ребро равно 4.
Источники:
а) Пусть — середина ребра
Рассмотрим плоскость
— она
сечет призму по прямоугольнику
и содержит
Следовательно,
точка
пересечения отрезка
и плоскости
лежит на линии
пересечения плоскостей
и
Эта линия пересечения —
прямая
где
— точка пересечения
и
Следовательно,
Так как — точка пересечения медиан
то
Рассмотрим прямоугольник
В нем
следовательно,
Что и требовалось доказать.
б) Для искомого объема имеем:
Так как
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
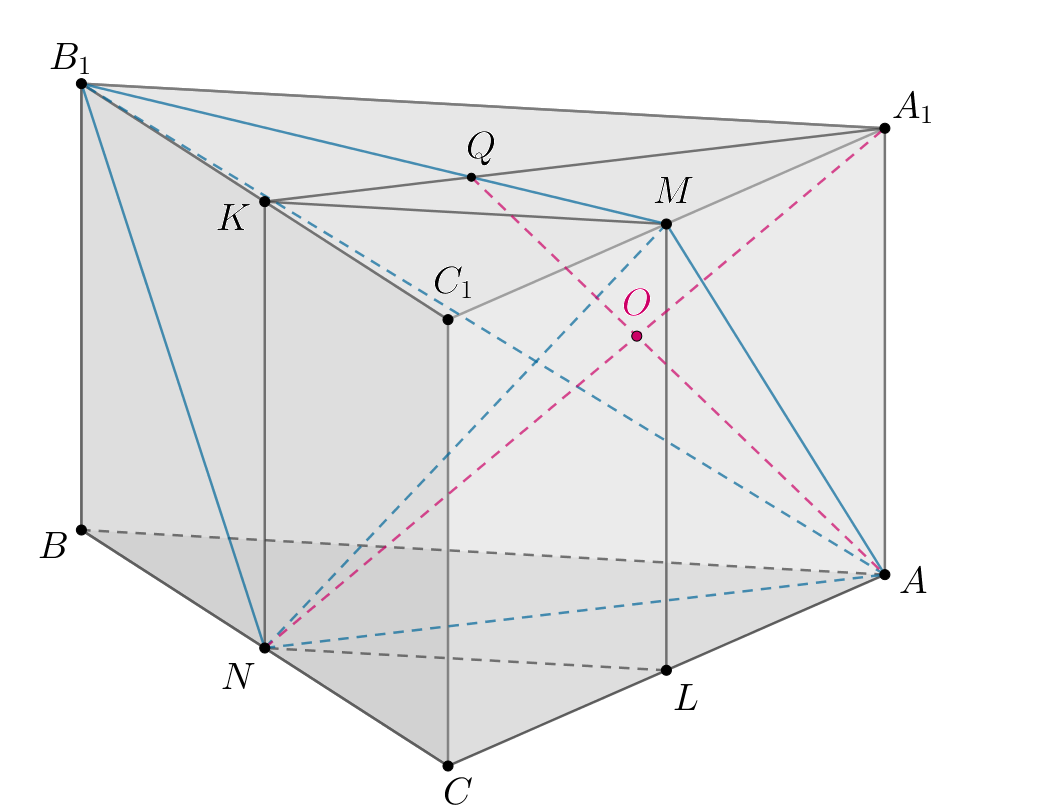
В прямоугольном параллелепипеде известно, что
Через точки
и
параллельно
проведена
плоскость, пересекающая ребро
в точке
а) Докажите, что — середина
б) Найдите расстояние от точки до плоскости сечения.
Источники:
а) Назовем плоскость, проходящую через и
параллельно
плоскостью
Рассмотрим плоскость
Эта плоскость содержит
и пересекает
в середине — точке
Сечение параллелепипеда этой плоскостью —
прямоугольник
Проведем через точку
прямую
Тогда
Следовательно,
— сечение параллелепипеда плоскостью

Так как — середина
то
— точка пересечения диагоналей
параллелепипеда, следовательно,
— середина диагонали
Значит, по
теореме Фалеса для
где
имеем:
— середина
Что и
требовалось доказать.
б) Рассмотрим многогранник Его объем равен половине объема
параллелепипеда:
Если из этого объема вычесть объемы
пирамид
и
каждый из которых равен
то
получим объем пирамиды
С другой стороны, если — расстояние от точки
до плоскости
то объем пирамиды
равен
Следовательно
Из этого равенства можно найти если найти площадь сечения.
По теореме Пифагора
Пусть Тогда по теореме косинусов из
Тогда Так как
— параллелограмм (плоскость
пересекает параллельные грани параллелепипеда по параллельным прямым), то
получаем
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,
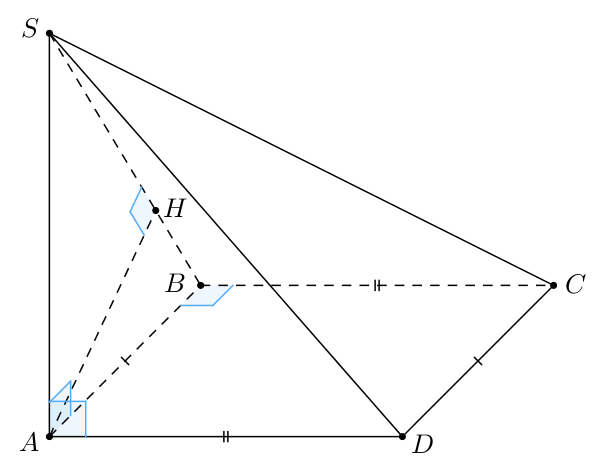
б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,
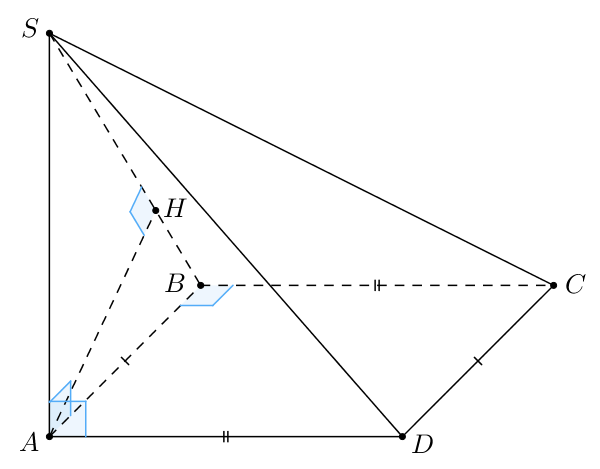
б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них имеем:
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,

б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
и
Длины боковых рёбер пирамиды
и
а) Докажите, что — высота пирамиды
б) Найдите расстояние от точки до плоскости
Источники:
а) Рассмотрим треугольники и
В них
Таким образом, по теореме, обратной теореме Пифагора, треугольники и
прямоугольные. Следовательно,
и
значит,
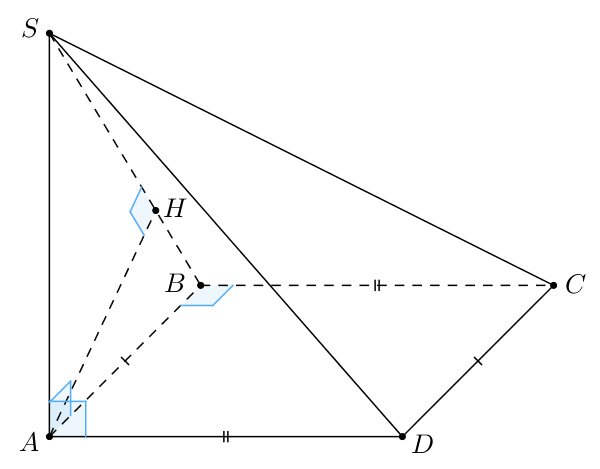
б) Проведем высоту в треугольнике
Заметим, что так как
и
так как
— прямоугольник. Тогда
Значит, Также
по построению. Тогда
Таким образом,
— расстояние от
до
В прямоугольном треугольнике
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



