14.03 Задачи формата ЕГЭ на многогранники. Пирамида, призма
Ошибка.
Попробуйте повторить позже
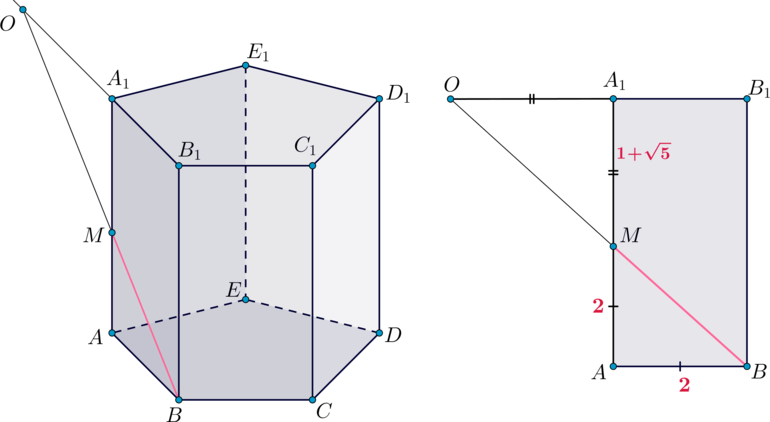
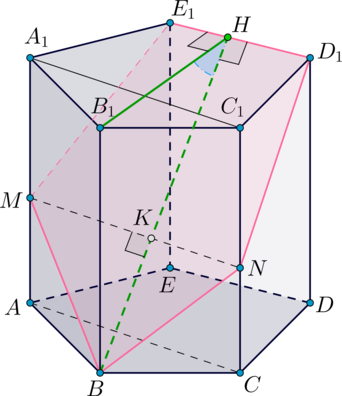
Дана правильная пятиугольная призма, сторона основания которой равна , а боковое ребро равно
. На ребре
на расстоянии
от точки
взята точка
.
1) Постройте сечение призмы плоскостью .
2) Найдите угол между плоскостью и плоскостью основания призмы.
Замечание: отношение диагонали правильного пятиугольника к его стороне равно
1) Назовем плоскость плоскостью
.
Найдем линию пересечения и плоскости
. Продлим лучи
и
до пересечения в
точке
. Тогда мы имеем две точки
и
в плоскости
, следовательно,
– линия
пересечения
и
.
Определим, где пересекает прямая пятиугольник
(и пересекает ли вообще).
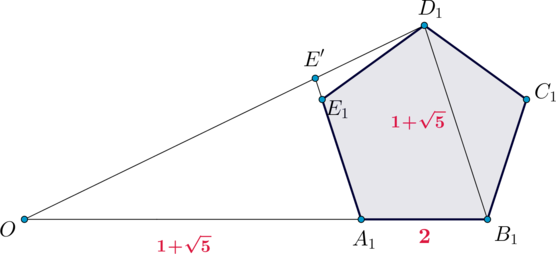
Рассмотрим плоскость . Так как
, то
равнобедренный. Так как
(по двум углам), то
тоже равнобедренный, следовательно,
.
Рассмотрим теперь плоскость :
Пусть прямая пересекает прямую
в точке
(неизвестно, внутри отрезка
или
снаружи). Так как по свойству правильного пятиугольника
, то
по
двум углам. Следовательно,
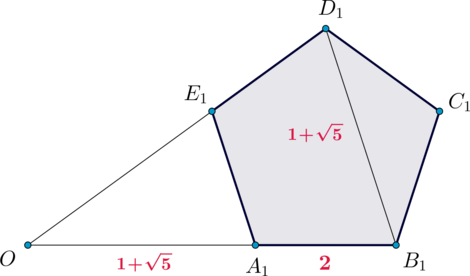
Таким образом, нам осталось найти точку пересечения плоскости с ребром
.
Рассмотрим плоскость . Она пересекает плоскость
по прямой
, параллельной
прямой
, которая в свою очередь является линией пересечения
и
. Следовательно,
пересечет
по прямой, параллельной
. Таким образом, в плоскости
проведем
прямую
, где
– точка пересечения этой прямой с
. Получили сечение
– пятиугольник.
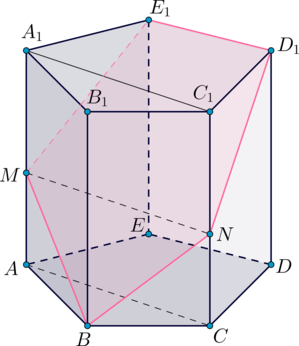
2) Так как , то
, следовательно,
. Аналогично
. Следовательно, перпендикуляр из
на
упадет в середину
- точку
.
Перпендикуляр из
на
упадет в середину
– точку
(по свойству равнобедренной
трапеции: отрезок, соединяющий середины оснований равнобедренной трапеции, перпендикулярен
основаниям). Следовательно,
.
По свойству правильного пятиугольника . Следовательно,
– линейный угол
двугранного угла, образованного плоскостями
и основания.
прямоугольный (
), следовательно,
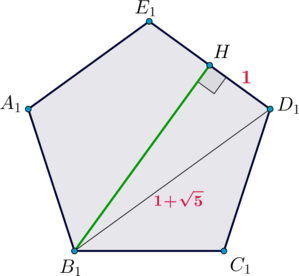
Из прямоугольного
2)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




