14.03 Задачи формата ЕГЭ на многогранники. Пирамида, призма
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде сторона основания
равна 12, а боковое ребро
равно
Через вершину
проведена плоскость
перпендикулярная прямой
и пересекающая ребро
в точке
а) Докажите, что плоскость делит высоту
пирамиды
в отношении
считая от вершины
б) Найдите расстояние между прямыми и
а) Прямая так как
принадлежит плоскости
перпендикулярной
Пусть
пересекает
в точке
тогда нам нужно доказать, что
Рассмотрим треугольник Его сторона
равна
как диагональ квадрата со стороной 12. Получили,
что
Следовательно, треугольник равносторонний. Поскольку
и
— его высоты, а значит, и медианы, то медиана
делит медиану
в отношении
считая от точки
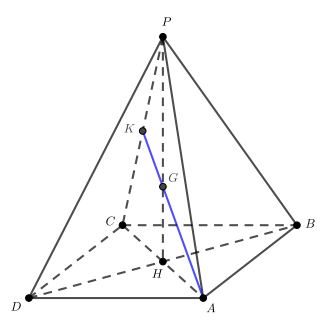
б) Отрезок является проекцией отрезка
на плоскость основания. Пусть
— проекция середины
отрезка
на основание пирамиды. Тогда
— середина
и
откуда
Из этого следует, что прямая
параллельна плоскости
Таким образом, расстояние между прямыми и
равно расстоянию между прямой
и плоскостью
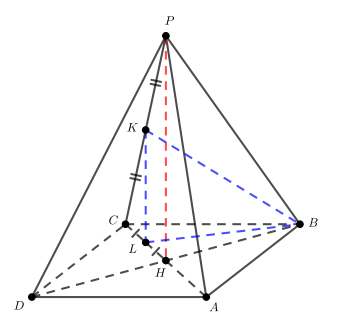
Рассмотрим высоту из вершины
треугольника
Имеем
а также
перпендикулярна прямым
(так как
и
плоскости
Тогда длина
— это и есть расстояние между прямой
и плоскостью
Далее имеем:
Тогда по теореме Пифагора для прямоугольного треугольника
Значит, окончательно из прямоугольного треугольника
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием прямой треугольной призмы является прямоугольный треугольник
причем
Диагонали
боковых граней
и
равны 26 и 10 соответственно,
а) Докажите, что — прямоугольный.
б) Найдите объем пирамиды
а) Так как
то по теореме о трех перпендикулярах
Следовательно,
—
прямоугольный.
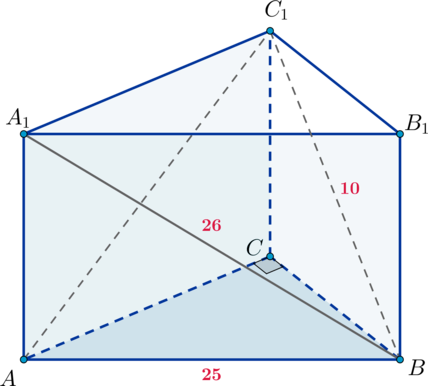
б) Заметим, что и
следовательно, по признаку перпендикулярности прямой и плоскости
Следовательно,
— высота пирамиды
с основанием
Так как — прямоугольный, то
По теореме Пифагора имеем:
Тогда искомый объем равен

б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
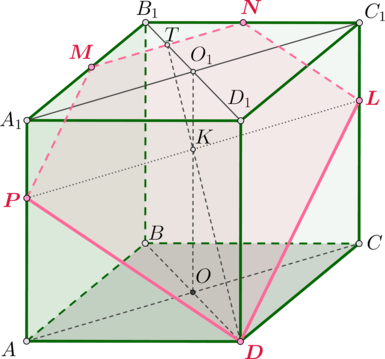
Дан прямоугольный параллелепипед .
– точка пересечения диагоналей грани
,
– точка пересечения диагоналей грани
, а
– середина ребра
.
а) Доказать, что сечение параллелепипеда плоскостью - пятиугольник.
б) Найти отношение длин отрезков, на которые делит плоскость ребро
, если
.
а) Построим сечение параллелепипеда плоскостью .
Т.к. плоскость
пересечет плоскость
по прямой,
параллельной
(пусть
- линия пересечения плоскостей
и
; если
не может быть параллельна
).
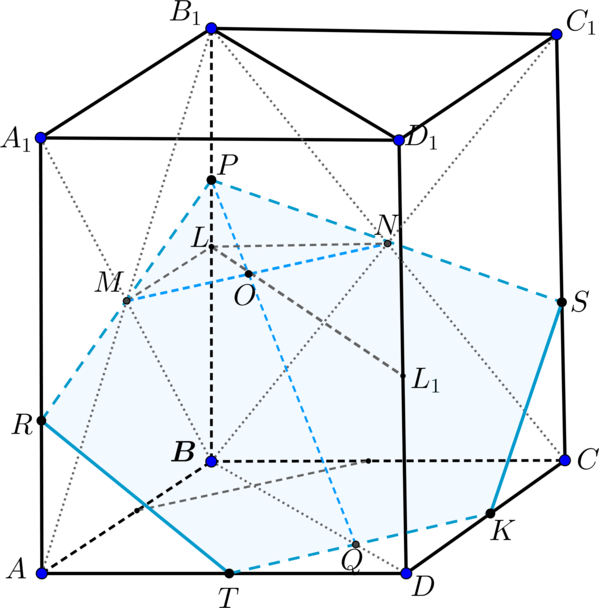
Пусть лежит на
, значит,
– середина
.
Рассмотрим сечение . Эта плоскость пересекает
и
в их серединах.
Пусть
– середина
,
– середина
. Прямая
пересекает ребро
в
точке
. Прямая
, таким образом,
– искомое
сечение.
б) Без ограничения общности можно считать, что . Таким образом,
.

. Точка
лежит на отрезке
, где
– середина
,
– середина
.
Найдем
.
– прямоугольный треугольник, причем
.
как медиана прямоугольного треугольника, проведенная к гипотенузе.
.
– равнобедренный
– равнобедренный (т.к.
)
.
б)
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде двугранные углы при ребрах
и
равны. Известно также, что
а) Докажите, что
б) Найдите объем пирамиды, если двугранные углы при ребрах и
равны
а) Рассмотрим пирамиду В ней по условию
Так как и
— равнобедренные, причем
— общее
основание, то высоты к основаниями попадут в одну точку — в середину
стороны
Тогда
Таким образом,
—
линейный угол двугранного угла

Аналогичным образом строится угол — линейный угол двугранного
угла
где
— середина
Таким образом,
Так как по трем сторонам, то
Аналогично
Значит,
и
— равнобедренные и подобные по двум
пропорциональным сторонам и углу между ними.
Заметим, что плоскости и
имеют две общие точки —
это точки
и
Следовательно, они пересекаются по прямой
Отрезок
— это высота в
и
к основаниям
и
соответственно. Следовательно, эти треугольники равны. Следовательно,
Что и требовалось доказать.
б)

Из пункта а) также следует, что
Так как двугранные углы равны то
и
—
равносторонние.
Пусть
Проведем высоту пирамиды Так как
то по теореме о
трех перпендикулярах
Таким образом, точка
должна
лежать на
причем на середине, так как
— равносторонний.
Тогда
Найдем по теореме Пифагора из
Таким образом,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании треугольной пирамиды лежит равносторонний треугольник
.
Все боковые грани наклонены к плоскости основания под углом
. Пирамида не является
правильной.
а) Докажите, что высота пирамиды падает в центр вневписанной для треугольника
окружности.
б) Найдите объем пирамиды, если , а сторона основания равна
.
а) Пусть – высота пирамиды. Проведем перпендикуляры
к прямым
соответственно. По теореме о трех перпендикулярах наклонные
также будут
перпендикулярны этим прямым. Следовательно, по определению
— линейные
углы двугранных углов между боковыми гранями и основанием. Т.к. эти углы равны, то
по катету и острому углу (
– общий катет).
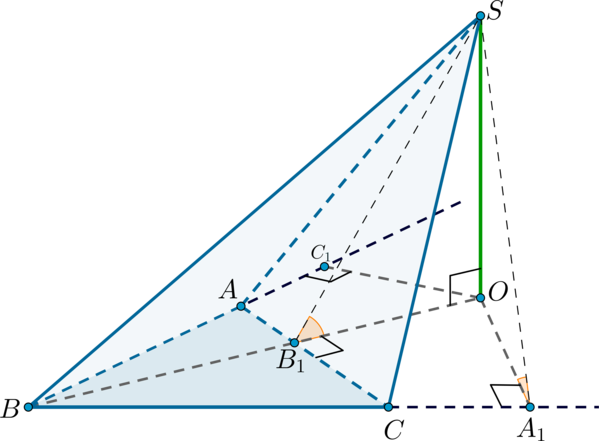
Таким образом, . Таким образом, тока
равноудалена от прямых
. Значит, это либо центр вписанной в
окружности, либо центр вневписанной
окружности (касающейся стороны и продолжений двух других сторон). Т.к. пирамида не является
правильной, то первый вариант не подходит, чтд.
б) Обозначим . Пусть для определенности
– центр окружности, касающейся
стороны
и продолжений сторон
и
. Тогда
лежит на биссектрисе угла
.
Следовательно,
– биссектриса, а т.к.
– правильный, то
. Следовательно, точка
лежит на биссектрисе
.
Значит, . Т.к. отрезки касательных, проведенных из одной точки, равны, то
. Следовательно,
. К тому же
(как половина
).
Значит,
Следовательно, . Из прямоугольного
Таким образом, объем пирамиды равен
б)
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная призма сторона основания которой равна 4, а боковые ребра равны 5. Точки
и
— середины отрезков
и
соответственно. Плоскость
проходит через точки
и
а) Докажите, что плоскость делит ребро
призмы в отношении
считая от точки
б) Найдите угол между плоскостью и плоскостью
а) Из условия следует, что призма прямая и основания являются квадратами.
Так как — средняя линия в
то
Тогда
плоскость
пересечет плоскость
по прямой
параллельной
прямой
В противном случае прямая
и плоскость сечения имеют
общие точки, но это невозможно, поскольку прямая
параллельна
прямой
плоскости
, а значит параллельна и самой плоскости
сечения.
Таким образом, найдем точку, в которой плоскость пересекает
плоскость
Пусть плоскость пересекает
в точке
Тогда
Если
и
— точки пересечения диагоналей оснований, то прямые
и
лежат в плоскости
Пусть
— точка их пересечения.
Тогда
— искомая точка пересечения плоскости
и плоскости
Проведем через точку прямую
параллельно
Пусть она пересекла
прямую
в точке
прямую
в точке
Таким образом, получили
сечение
призмы плоскостью

Так как — средняя линия треугольника
то она пересекает
в её середине, то есть
— середина
Значит,
В плоскости рассмотрим треугольники
и
В них
как вертикальные и
Значит,
Запишем отношение их подобия:
С другой стороны, так как
б) Так как линии пересечения параллельных плоскостей третьей плоскостью
параллельны между собой, то общая прямая плоскости сечения и нижнего
основания призмы параллельна а значит, параллельна
и параллельна
Найдем две прямые, перпендикулярные
и построим соответствующий
линейный угол.
Заметим, что следовательно, так как
то и
по теореме о трех перпендикулярах. Значит,
равен углу
между плоскостями
и
По теореме Фалеса имеем:
Так как то
Следовательно,
Кроме того,
Тогда окончательно имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
- прямая треугольная призма,
,
.
–
середины ребер
и
соответственно.
– такие точки на ребрах
и
соответственно, что
.
а) Построить сечение призмы плоскостью , параллельной прямой
и проходящей через точки
и
.
б) Найти площадь сечения призмы плоскостью .
а) 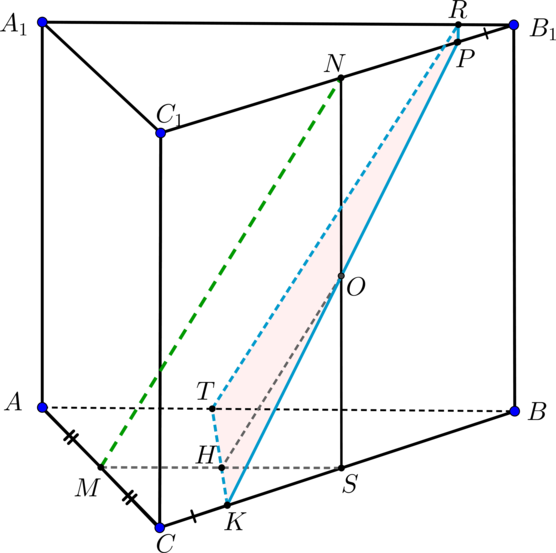
Если прямая параллельна некоторой прямой, лежащей в
. Проведем
. В плоскости
проведем
. Тогда прямая
. Так как плоскости
и
параллельны, то
пересечет плоскость
по прямой, параллельной
. Следовательно, проведем
. Таким образом,
– искомое
сечение (трапеция).
б) Заметим, что . Т.к.
– средняя линия треугольника
. Так как
, то по теореме косинусов
. Таким образом, по обратной теореме Пифагора треугольник
–
прямоугольный, следовательно,
. Таким образом, по теореме о трех перпендикулярах, из
того, что
.
Проведем . Из подобия треугольников
и
следует, что
. Т.к.
. Таким образом найдена высота трапеции
.
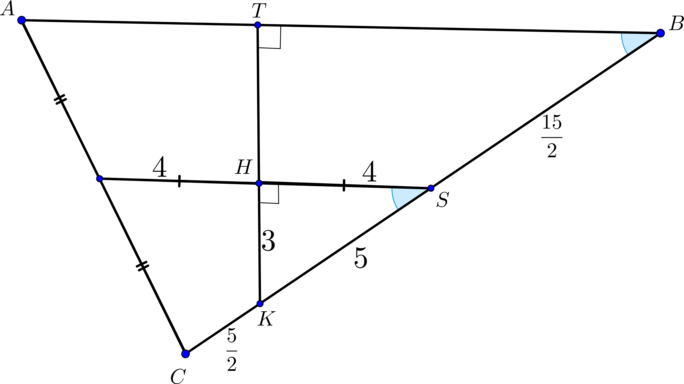
Найдем основания трапеции и
.
.
.
Таким образом,
б)
Ошибка.
Попробуйте повторить позже
Дан правильный тетраэдр
— такая точка на высоте
что
Плоскость
проходит через точки
и
параллельно
медиане
треугольника
и пересекает ребро
в точке
а) Докажите, что
б) Найдите угол между плоскостями и
а)
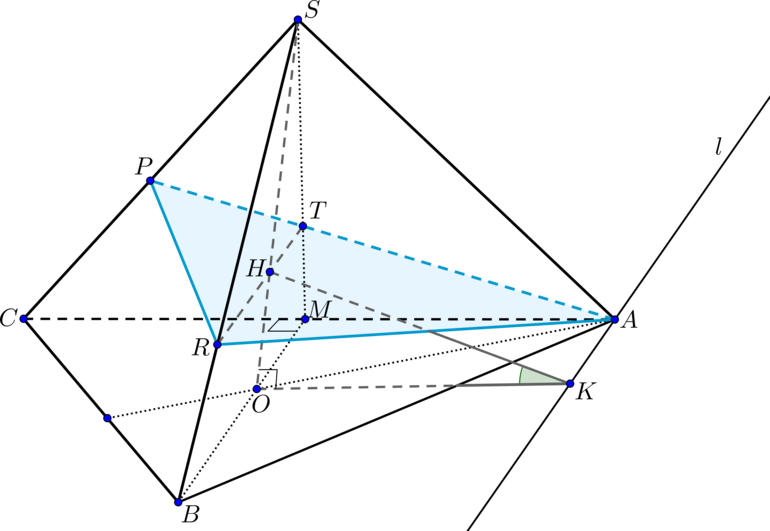
Правильный тетраэдр — это правильная треугольная пирамида, у которой все
ребра равны. Пусть ребро пирамиды равно
Так как пирамида правильная, то высота падает в точку пересечения
медиан
Рассмотрим плоскость
точка
лежит в этой
плоскости. Так как плоскость
параллельна
то она пересекает плоскость
по прямой, параллельной
Проведем
Тогда по теореме Фалеса
Прямая пересечет
в точке
— сечение пирамиды
плоскостью
Напишем теорему Менелая для и прямой
Из этого равенства находим, что
б) Докажем, что линия пересечения плоскостей и
параллельна
прямой
Пусть это не так: пусть
— линия пересечения
и
и
Тога прямая
следовательно, не может быть
параллельна
Получили противоречие, следовательно,
Заметим, что
прямая
проходит через точку
Построим линейный угол двугранного угла между и
Так
как
проведем
следовательно, по теореме о трех
перпендикулярах
Таким образом,
— искомый угол.
Найдем
Тогда
Значит,
Найдем
следовательно,
Так как
имеем
Таким образом,
— параллелограмм,
следовательно,
Треугольник — прямоугольный, следовательно,
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте а) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с вершиной
стороны
основания которой равны
а боковые ребра равны 21.
а) Постройте сечение пирамиды плоскостью, проходящей через точку и
середину ребра
параллельно прямой
б) Найдите площадь построенного сечения.
а) Пусть — середина ребра
— высота пирамиды (падает в точку
пересечения диагоналей основания).
Необходимо построить прямую, лежащую в плоскости сечения и параллельную
Рассмотрим плоскость
Прямая
пересекает
в точке
Теперь рассмотрим
Проведем в этой плоскости через точку
прямую, параллельную
Пусть она пересечет ребра
и
в точках
и
соответственно. Таким образом,
— искомое сечение.
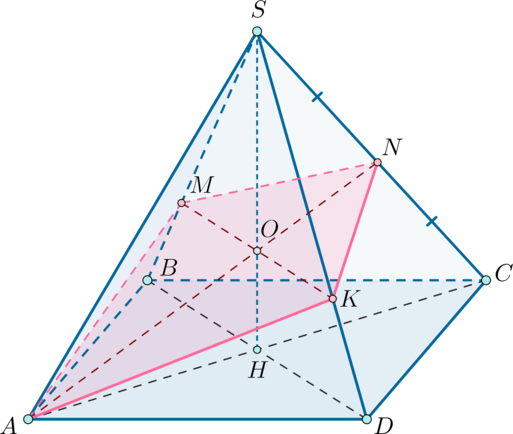
б) Заметим, что по теореме о трех перпендикулярах (так как
)
Так как
то
следовательно,
Следовательно, у четырехугольника
диагонали взаимно
перпендикулярны. Значит, его площадь можно найти как
Заметим сразу, что
Рассмотрим плоскость
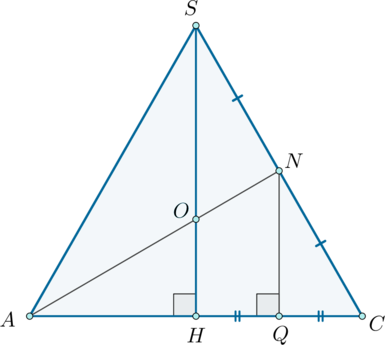
По теореме Менелая:
(это нам понадобится позже для поиска )
Проведем Тогда из подобия
и
— середина
следовательно,
Тогда по теореме Пифагора
Рассмотрим Так как
то
Следовательно, площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде с основанием
на медиане
основания
взята точка
так, что
Через точку
проведена плоскость
которая перпендикулярна прямой
и пересекает
боковые ребра
и
в точках
и
соответственно.
а) Докажите, что
б) Найдите объем пирамиды, вершиной которой является точка а
основанием — сечение пирамиды
плоскостью
если известно, что
а) Пусть — высота пирамиды,
— точка пересечения медиан.
Следовательно,
Так как по условию то можно обозначить
Тогда
Следовательно,
Так как перпендикулярна плоскости
то нужно построить две
пересекающиеся прямые в плоскости
которым
будет перпендикулярна.
Первая прямая: так как то проведем через точку
прямую
Тогда
Вторая прямая: так как то
Следовательно, проведем
тогда
Следовательно, проходит через точки

Заметим, что пересечет плоскость
по прямой, параллельной
(в
противном случае
будет иметь общую точку с
что невозможно, так как
Следовательно, и проходит через
Из подобия
Из подобия
б) Рассмотрим пирамиду
— высота этой пирамиды,
—
трапеция
Следовательно,
Так как то
Следовательно,
Из подобия
Из пункта а) Из подобия
Следовательно,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Ребра пирамиды
попарно перпендикулярны.
.
а) Докажите, что пирамида правильная.
б) Найдите площадь сечения , если точки
и
лежат на ребрах
и
соответственно, причем
.
а) Для того, чтобы доказать, что пирамида является правильной, нужно доказать, что в основании
пирамиды находится правильный многоугольник, а боковые ребра равны.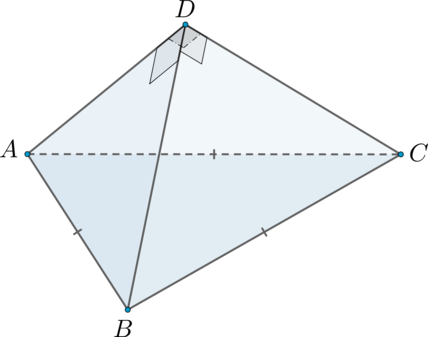
Возьмем за основание – он правильный по условию.
Осталось доказать, что .
Рассмотрим и
. Они прямоугольные и равны по катету и гипотенузе. Следовательно,
. Аналогично рассматривая другие боковые грани, доказываем, что
.
Следовательно,
, чтд.
б) Заметим, что так как и боковые грани – равные треугольники, то
.
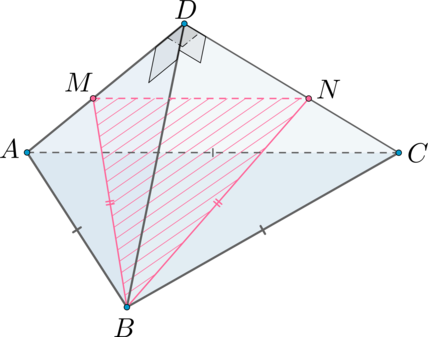
Так как , то по теореме Фалеса
, также
.
Из подобия следует:
Так как
Рассмотрим прямоугольный
Рассмотрим теперь

Так как он равнобедренный, то высота
б)
Ошибка.
Попробуйте повторить позже
– правильный тетраэдр с ребром
.
– такие точки на ребрах
соответственно, что
.
а) Постройте сечение пирамиды плоскостью .
б) Найдите площадь сечения тетрадра плоскостью .
а) По условию представляет собой правильную треугольную пирамиду, все ребра которой
равны
. Построим сечение пирамиды плоскостью
. Продлим прямую
до
пересечения с прямой
– получим точку
. Соединив точки
и
, получим линию
пересечения основания – отрезок
. Таким образом, сечением является четырехугольник
.
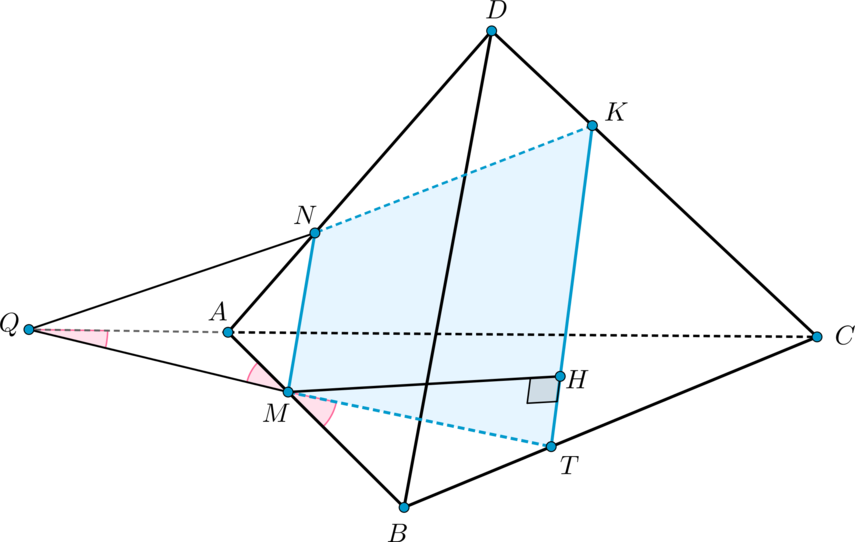
б) По теореме Менелая для и прямой
имеем:
По условию . Т.к.
и
. Следовательно,
, тогда
. Следовательно,
. Заметим, что
по
углу и двум прилежащим сторонам, следовательно,
. Также заметим, что так как
, то
. Также и
. Следовательно,
– равнобедренная
трапеция.
Основания ,
, по теореме Пифагора
. Следовательно,
если провести высоту
, то
. Тогда по теореме Пифагора
. Следовательно,
б)
Ошибка.
Попробуйте повторить позже
– четырехугольная пирамида, в основании которой лежит квадрат
, а две боковые
грани
и
представляют собой прямоугольные треугольники с прямым углом
.
1) Проведите плоскость через точку пересечения диагоналей основания параллельно грани
.
2) Найдите площадь сечения пирамиды плоскостью , если
.
1) Пусть . Две плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Заметим, что т.к. .
Проведем в плоскости прямую
. Т.к.
– середина
, то по теореме Фалеса
– середина
. Через точку
в плоскости
проведем
(следовательно,
–
середина
). Таким образом, плоскость, проходящая через прямые
и
, и будет искомой
плоскостью.
Необходимо найти сечение пирамиды этой плоскостью. Соединив точки и
, получим прямую
.
Т.к. ,то
пересечет плоскость
по прямой
(если
, то
, что невозможно ввиду их параллельности).
Таким образом, – искомое сечение, причем
это трапеция.
2) Т.к. все точки – середины отрезков
соответственно,
то:
а)
б)
в)
Заметим, что по теореме о трех перпендикулярах . Таким образом,
– прямоугольная трапеция.
1) Рисунок.
2)
Ошибка.
Попробуйте повторить позже
Точка лежит на ребре
треугольной пирамиды
причем
а) Постройте сечение пирамиды плоскостью, проходящей через точку и
середины ребер
и
б) Найдите, в каком отношении плоскость сечения делит ребро
а) Обозначим плоскость сечения через
Все точки прямой принадлежат плоскости
при этом
Тогда
принадлежит плоскости
Все точки прямой принадлежат плоскости
при этом
Тогда
принадлежит
плоскости
Искомое сечение
![]()
б) Запишем теорему Менелая для треугольника и прямой
учитывая, что
Запишем теорему Менелая для треугольника и прямой
учитывая, что
и
Поделив первое на второе, получим
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с основанием
стороны основания которой равны
Точка
— середина ребра
Тангенс угла между прямыми
и
равен
а) Пусть — центр основания пирамиды. Докажите, что прямые
и
перпендикулярны.
б) Найдите высоту данной пирамиды.
а) Пирамида правильная, поэтому центр основания является основанием высоты пирамиды из вершины
Тогда имеем:
Кроме того, как диагонали квадрата
Получили, что
Так как то
Таким образом,
![]()
б) По условию известно, что тангенс угла между прямыми и
равен
Отрезок
параллелен
как средняя линия в
следовательно, тангенс угла
между прямыми
и
также
равен
Кроме того,
как катеты равнобедренного прямоугольного треугольника со стороной
В пункте а) мы доказали, что тогда в прямоугольном треугольнике
Треугольник прямоугольный,
— его медиана, следовательно,
По теореме Пифагора для треугольника
![]()
б) 5
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте а) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Точки и
— середины ребер соответственно
и
треугольной призмы
а) Постройте сечение призмы плоскостью, проходящей через точки
и
б) В каком отношении плоскость сечения делит ребро
Обозначим плоскость сечения через
Все точки прямой принадлежат
при этом
Тогда
принадлежит
Все точки прямой принадлежат
при этом
Тогда
принадлежит
Тогда — искомое сечение.
![]()
б) Так как то
по стороне и прилежащим к ней углам. Тогда
Запишем теорему Менелая для треугольника и прямой
учитывая, что
и
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основание пирамиды — параллелограмм
с центром
. Точка
— середина отрезка
а) Постройте сечение пирамиды плоскостью, проходящей через точку параллельно прямым
и
б) В каком отношении плоскость сечения делит ребро
а) Обозначим через плоскость сечения.
- По условию
, следовательно,
пересекает плоскость
, содержащую прямую
, по прямой, проходящей через точку
и параллельной
. Проведем через
прямую, параллельную
, точки
и
— ее пересечения с
и
соответственно — лежат в плоскости
.
- По условию
, следовательно,
пересекает плоскости
и
, содержащие
, по прямым, параллельным
. Проведем через
и
прямые, параллельные
, тогда
и
— точки пересечения этих прямых с
и
соответственно, эти точки также принадлежат
.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
- Все точки прямой
принадлежат
, при этом
. Тогда
принадлежит
.
Получили, что — искомое сечение.
![]()
б) По построению плоскость сечения параллельна прямой . Отрезок
лежит как в плоскости сечения, так и в
плоскости
, значит, он параллелен
. Тогда по теореме Фалеса
Отрезок равен четверти диагонали
параллелограмма, следовательно, искомое отношение равно
.
б)
Ошибка.
Попробуйте повторить позже
В основании четырёхугольной пирамиды лежит прямоугольник
со сторонами
При этом
известны длины некоторых боковых ребер:
а) Докажите, что — высота пирамиды
б) Найдите угол между прямой и плоскостью
а) Рассмотрим треугольник
Следовательно, треугольник прямоугольный и
Рассмотрим треугольник
Следовательно, треугольник прямоугольный и
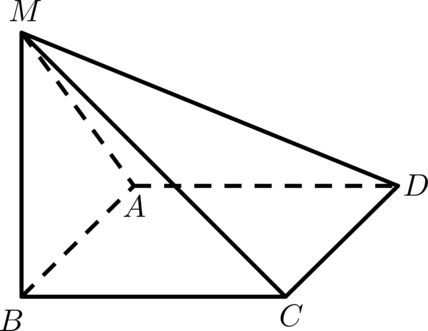
Таким образом, прямая перпендикулярна двум пересекающимся прямым плоскости
Тогда прямая
перпендикулярна плоскости
и
— высота пирамиды
б) По пункту а) прямая значит,
По условию
значит,
по признаку
перпендикулярности прямой и плоскости.
Следовательно, — проекция
на плоскость
Тогда угол
и есть угол между
и плоскостью
По теореме Пифагора в треугольнике
Тогда найдем искомый угол:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании прямой треугольной призмы лежит равнобедренный треугольник
с основанием
Точка
— середина ребра
а точка
ребра
такая, что
а) Докажите, что прямая перпендикулярна прямой
б) Найдите угол между прямой и плоскостью
если
и
а) Пусть точка — середина ребра
точка
— середина ребра
Так как треугольник
равнобедренный, то
— медиана и высота, то есть
Далее имеем:
Значит, треугольник подобен треугольнику
по общему углу
и отношению прилежащих к нему
сторон
Тогда
![]()
Отрезок перпендикулярен плоскости
так как призма прямая, следовательно,
является проекцией
на плоскость
Получаем, что прямая
перпендикулярна проекции
а значит по теореме о трех
перпендикулярах и наклонной
Что и требовалось доказать.
б) Пусть — высота треугольника
Так как плоскости
и
перпендикулярны, то отрезок
перпендикулярен плоскости
Тогда
является проекцией
на плоскость
поэтому
и есть
искомый угол.
![]()
Вычислим двумя способами площадь треугольника Имеем:
Найдем угол в прямоугольном треугольнике
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной призме сторона основания
а боковое ребро
На ребрах
и
отмечены точки
и
соответственно так, что
а
а) Докажите, что прямые и
перпендикулярны.
б) Найдите угол между плоскостями и
а) По условию следовательно,
Далее, по прямым углам
и отношениям прилежащих к ним
катетов
Следовательно,
Из прямоугольного треугольника мы знаем, что
Тогда
![]()
Основанием правильной четырехугольной призмы является квадрат, а сама призма является прямоугольным
параллелепипедом, значит, отрезок перпендикулярен плоскости
Тогда
является проекцией наклонной
на плоскость
Так как
то по теореме о трех перпендикулярах
что и требовалось
доказать.
б) Поскольку то угол между плоскостями
и
равен углу между плоскостями
и
Эти плоскости пересекаются по прямой
![]()
В пункте а) мы уже доказали, что и
следовательно, острый угол
прямоугольного
треугольника
равен искомому углу между плоскостями
и
По теореме Пифагора в прямоугольном треугольнике имеем:
Тогда из прямоугольного треугольника имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



