14.17 Нахождение объема или площади поверхности
Ошибка.
Попробуйте повторить позже
Мало кто знает, но в своё время Дед Мороз тоже закончил мехмат МГУ — Мурманского Государственного Университета! В ту эпоху ЕГЭ ещё не было и для поступления Дед Мороз сдавал внутренние вступительные экзамены.
Дан куб в который вписан шар с центром в точке
На
диагонали
отмечена точка M так, что
Точка
—
середина диагонали
а) Докажите, что центр шара принадлежит плоскости
б) Из точек и
опустили перпендикуляры
и
на плоскость
Найдите объём пирамиды
если ребро куба равно
8.
Попробуйте решить оба пункта, и кто знает, возможно, и вы однажды станете студентом МГУ!!!
а)
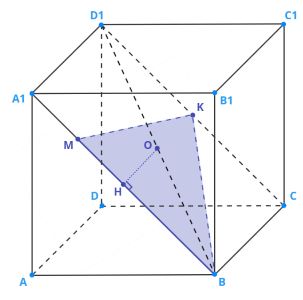
1. Шар вписан в куб, центром этих фигур является одна и та же точка, поэтому работать будем именно с центром куба. Центр куба — точка пересечения его диагоналей.
2. Пусть — середина диагонали
Теперь следует доказать, что точка
принадлежит плоскости
3. Диагональ лежит в плоскости
В этой же плоскости лежат и
три точки плоскости
то есть точка
лежит в той же плоскости, что и
все точки
Ч.Т.Д.
б)
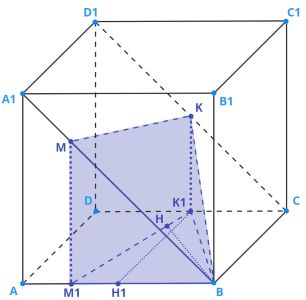
1. Проведём перпендикуляр к прямой
2. следовательно,
перпендикулярно любой прямой,
лежащей в плоскости
то есть
3. и
означают, что
То есть
— высота пирамиды. Найдем её длину через метод площадей для
4. Проведём перпендикуляр к
Его длина равна длине стороны
так как
— прямоугольник.
5. Из подобия , получаем
откуда поскольку
— куб, у него все
рёбра равны.
6. Аналогично находим, что откуда
и
— середины
сторон
и
соответственно.
7. По теореме Пифагора для
8. По методу площадей для вычислим высоту
9. Основание пирамиды — четырёхугольник Прямые
и
перпендикулярны плоскости
значит они параллельны и
на самом деле — трапеция.
10. Из тезисов и
выводим, что
То есть
— высота трапеции.
11. Найдём площадь основания пирамиды:
12. Найдём объём пирамиды:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




