14.17 Нахождение объема или площади поверхности

а)

1) Достроим усеченный конус до целого конуса. Тогда – высота, – образующая всего конуса; – образующая усеченного конуса, – осевое сечение усеченного конуса, – диагональ этого сечения, которая перпендикулярна .
– угол между образующей и плоскостью нижнего основания.
 

 

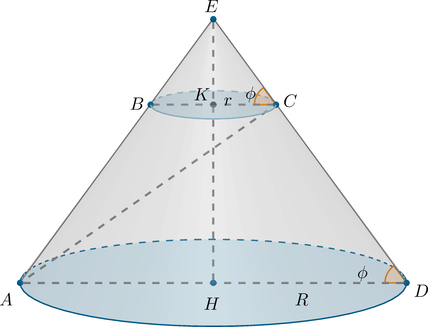
Обозначим за и – радиусы нижнего и верхнего оснований усеченного конуса соответственно. Тогда из условия сумма длин окружностей оснований равна

2) Для того, чтобы найти площадь боковой поверхности усеченного конуса, нужно из площади боковой поверхности всего конуса вычесть площадь боковой поверхности маленького конуса:

Заметим, что и – прямоугольные, следовательно,

Значит, площадь боковой поверхности уже приобретает вид:

Необходимо найти .

 

3) Т.к. , то – прямоугольный, следовательно,

Из данных второго пункта мы можем сказать, что

Таким образом, имеем:

Но , следовательно, , следовательно,

Подставляя это значение для в , находим, что

Таким образом,

4) Значит, площадь боковой поверхности равна

б) Подставляя значения из условия и помня, что , найдем площадь боковой поверхности: