14.17 Нахождение объема или площади поверхности
Ошибка.
Попробуйте повторить позже
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, высота которой равна
, а величина плоского угла при вершине равна
. Вычислите эту площадь, если
,
.
Способ 1.
1) Рассмотрим правильную пирамиду ,
– высота (которая падает в точку
пересечения диагоналей основания),
.
Напомним, что у правильной пирамиды все боковые грани представляют собой равные равнобедренные
треугольники.
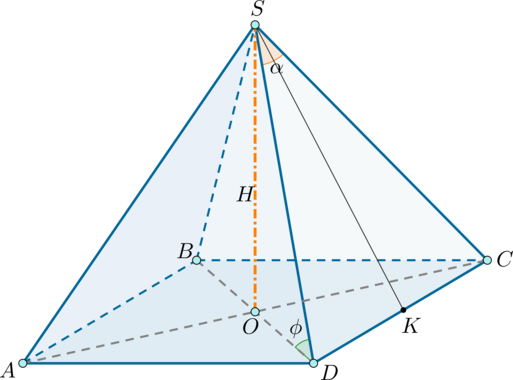
Введем вспомогательный угол между боковым ребром и основанием: .
Тогда , следовательно,
.
Тогда, т.к. площадь треугольника равна полупроизведению сторон на синус угла между ними,
2) Теперь необходимо выразить через данные в условии величины.
Проведем – медиану и высоту в равнобедренном
. Тогда
как диагональ квадрата, следовательно,
. В
:
Разделим равенство на равенство
и получим:
Тогда .
3) Таким образом,
4) Подставляя значения из условия, находим, что
Способ 2.
Пусть длина квадрата основания равна . Тогда
а
Выразим
квадраты длин
и
по теореме Пифагора для треугольника
Запишем теорему косинусов для
, выразив квадрат стороны
Подставим полученное выражение для в формулу
.
Выразим площадь треугольника
Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




