17.03 Задачи формата ЕГЭ

а) Очевидно, что основания перпендикуляров на прямые, содержащие противоположные стороны параллелограмма, и точка, из которой они опущены лежат на одной прямой. Мы не знаем точное положение точек, поэтому не будем им пользоваться. Возьмем пару прямых, содержащих противоположные стороны параллелограмма. Диагональ будет отрезком секущей для пары параллельных прямых, заключенным между ними. Пусть — точка выбранная на диагонали , и основания перпендикуляров. Получим картинку, приведенную ниже.

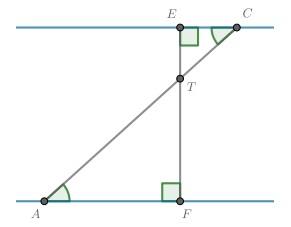
по трем углам с коэффициентом . То есть перпендикуляр между прямыми, содержащими противоположные стороны параллелограмма, делится точкой пересечения в том же отношении, что и диагональ. Это верно и для второго перпендикуляра. Получается, что перпендикуляры — это два пересекающихся отрезка, которые делятся точкой пересечения в одинаковом отношении (равном отношению на диагонали). Пусть второй перпендикуляр , тогда по двум сторонам и углу и — трапеция.

б) Заметим, что стороны параллелограмма, как и диагонали, являются отрезками секущих для двух параллельных прямых, а длины диагоналей трапеции из первого пункта являются расстояниями между парами противоположных сторон параллелограмма (т.к. перпендикулярны им). Во втором пункте нам фактически дано, что угол наклона этих секущих равен .

Обозначим длины сторон параллелограмма через и , тогда расстояния между соответствующими парами противоположных сторон (и длины диагоналей нашей трапеции соответственно) равны и . Найдем угол между диагоналями. Картинка будет иметь вид, приведенный ниже, где равен или в зависимости от того, на какой диагонали параллелограмма выбрана точка .

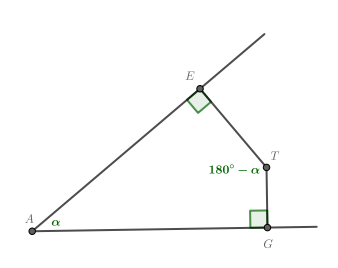
По сумме углов четырехугольника , соответствующий углу между диагоналями трапеции, равен . Тогда его синус равен синусу равен . Тогда площадь трапеции равна половине произведения диагоналей на синус угла между ними: