17.03 Задачи формата ЕГЭ
Ошибка.
Попробуйте повторить позже
Угол треугольника
равен
Сторона
является хордой окружности с центром
и радиусом
проходящей через центр окружности, вписанной в треугольник
а) Докажите, что около четырёхугольника можно описать окружность.
б) Известно, что в четырёхугольник можно вписать окружность. Найдите радиус
этой окружности, если
а) Пусть
Тогда по сумме углов
имеем:
Пусть точка — центр вписанной окружности
Мы знаем, что центром вписанной окружности треугольника является точка пересечения его биссектрис. Значит, —
биссектриса
а
— биссектриса
Следовательно,
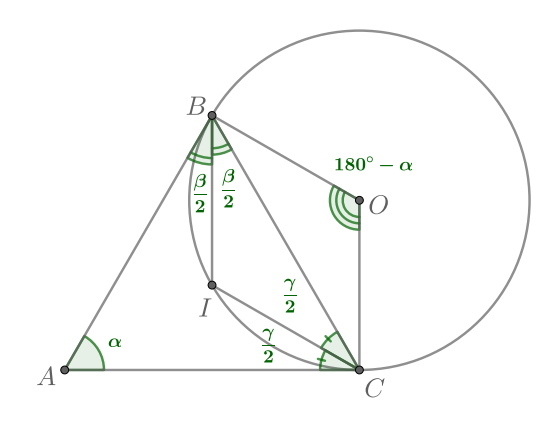
Углы и
вписаны в описанную окружность
и опираются на дуги
и
соответственно, поэтому
равны половинам их величин. Значит, величина дуги
равна
Рассмотрим центральный угол окружности, описанной вокруг треугольника
Он опирается на дугу
поэтому равен ей, так как является центральным. Значит,
Тогда рассмотрим четырехугольник . В нем сумма противоположных углов
и
равна
Значит, четырехугольник — вписанный.
б) Так как в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны, то
есть
Заметим, что как радиусы описанной окружности треугольника
значит,
Рассмотрим В нем
и
Следовательно,
является равносторонним. Тогда
имеем:
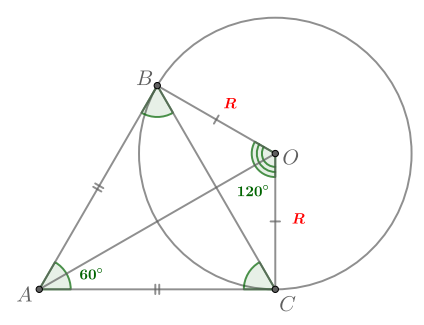
В предыдущем пункте мы доказали, что Тогда
Вернемся к четырехугольнику В нем
и
Значит,
— дельтоид. Осью симметрии
является прямая, содержащая диагональ
Тогда центр вписанной окружности, пусть это точка должен лежать на
Также в дельтоиде
диагональ
является биссектрисой углов
и
значит,
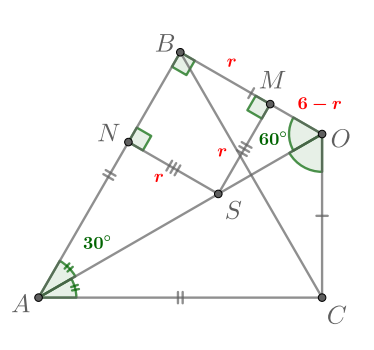
Тогда рассмотрим Он прямоугольный, так как по сумме углов треугольника
Пусть и
— радиусы вписанной окружности четырехугольника
проведенные к сторонам
и
соответственно. Тогда
и
следовательно,
— квадрат со стороной
Далее
имеем:
Рассмотрим треугольник В нем
и
тогда
Мы уже знаем, что и
значит,
Тогда искомый радиус окружности равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




