17.03 Задачи формата ЕГЭ

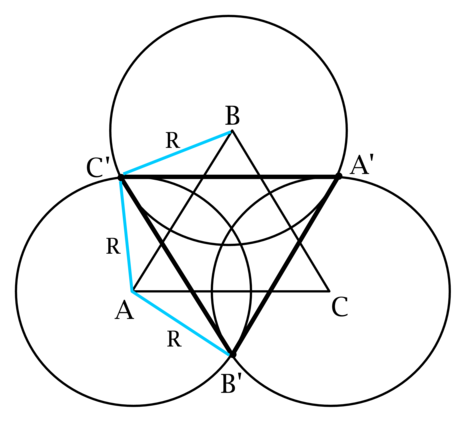
а) Обозначим вершины треугольника через , и как показано на рисунке. Пусть – центр треугольника .

Так как своими центром и радиусом любая окружность определяется однозначно, то точки , и однозначно определяются положениями точек , и и числом .

Так как поворот плоскости является движением (сохраняет любые расстояния), то при повороте плоскости на вокруг точки множество точек перейдёт само в себя, следовательно, и множество точек перейдёт само в себя.
 

 

Если бы одна из сторон треугольника была длиннее других его сторон, то при повороте плоскости множество не перешло бы в себя (иначе длинная сторона перешла бы в более короткую, но поворот плоскости – движение), следовательно, у нет стороны, которая длиннее других, следовательно, – равносторонний, а все равносторонние треугольники подобны.

 

б) Рассмотрим треугольник : , .

Этими данными треугольник определяется однозначно. Обозначим и запишем для него теорему косинусов:

так как треугольники и равны по трём сторонам, тогда .

По теореме косинусов в треугольнике :

Из основного тригонометрического тождества при учёте того, что :

Итого

следовательно, периметр равен