18.10 Алгебра. Задачи, решающиеся аналитически

1 способ.

Заметим, что не является решением этого уравнения, следовательно, можно разделить обе части равенства на и получим

Если исходное уравнение должно иметь ровно один корень на отрезке то новое уравнение должно иметь один корень на полуинтервале (выше сказали, что ).

Будем рассматривать параметр как переменную. Построим в системе координат множество решений системы. Если некоторая точка плоскости с координатами принадлежит этому множеству то для исходной задачи это означает, что если параметр принимает значение то будет одним из решений системы. Нас просят найти все такие значения параметра при каждом из которых одна точка вида , принадлежат множеству решений изображенному на плоскости Фактически это равносильно тому, что горизонтальная прямая имеет одну точку пересечения с множеством .

Множество представляет собой график функции . Исследуем эту функцию:

Производная равна нулю в точках , разрывна в точке , причем при производная положительна, следовательно, функция возрастает, а при производная отрицательна, следовательно, функция убывает.

Таким образом, так как , а при имеем , график функции выглядит следующим образом:

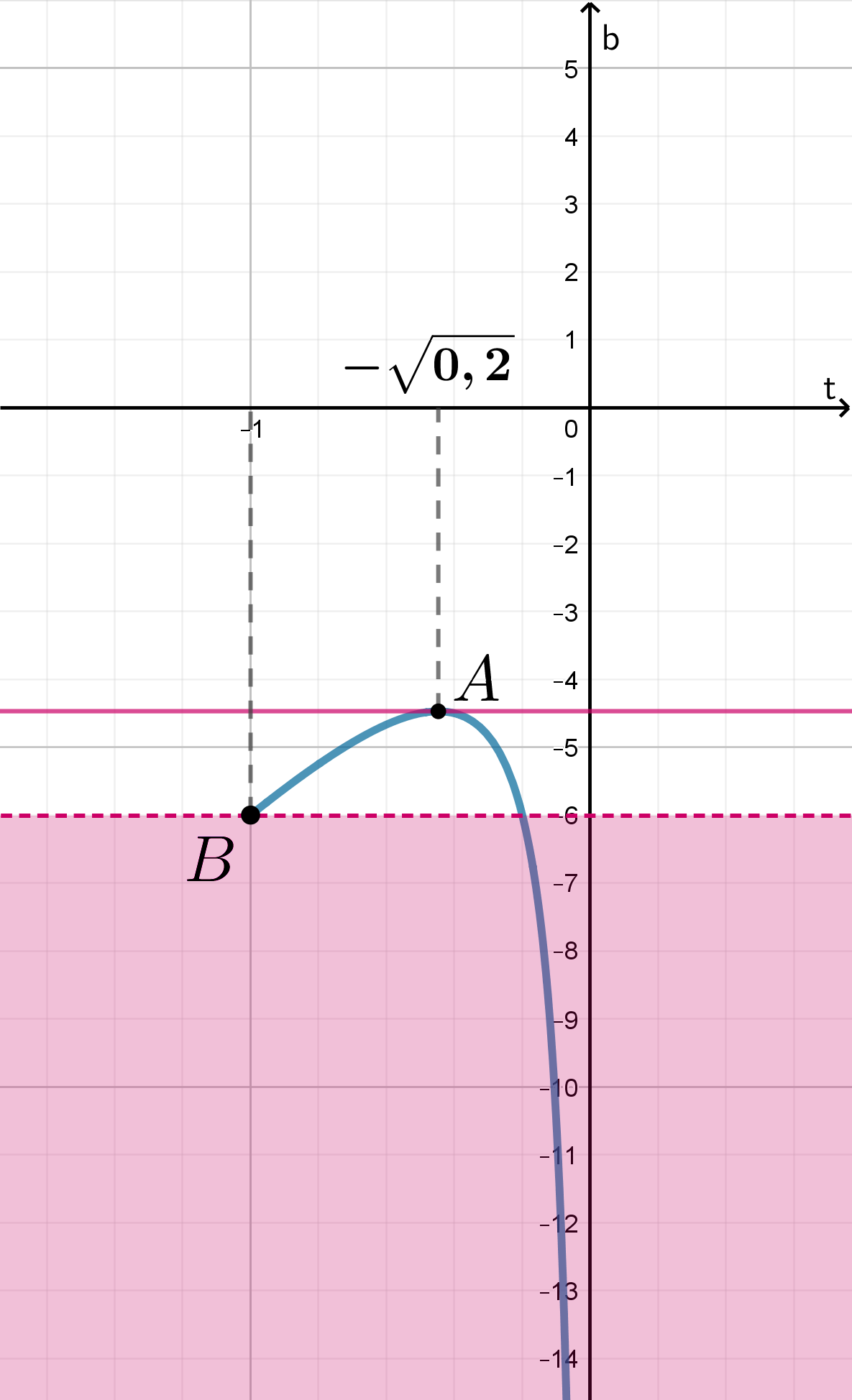
Розовым цветом показана область, в которой может находиться горизонтальная прямая , чтобы иметь с графиком на промежутке ровно одну точку пересечения.

Найдем : , следовательно,

Найдем : , следовательно,

Таким образом, или откуда или

2 способ.

Для начала заметим, что если , то .

Теперь сделаем замену , , тогда и исходное уравнение равносильно системе:

При этом, зная решение системы , можно найти корень исходного уравнения, сделав обратную замену:

То, что корень исходного уравнения лежит на промежутке , равносильно тому, что решение системы лежит на промежутке , так как

Тогда количество корней в исходном уравнении на отрезке будет совпадать с количеством корней в системе

Таким образом, достаточно найти такие значения , при которых система имеет ровно одно решение.

Квадратное уравнение имеет корни (необязательно различные) при . Обозначим их за и . По теореме Виета произведение корней равно , то есть оба корня одного знака.

Для того, чтобы система имела решение, один из корней должен лежать на отрезке , т.е. он не может быть положительным. Тогда оба корня уравнения должны быть отрицательными.

При этом также по теореме Виета сумма корней равна и должна быть отрицательной, откуда следует, что .

Рассмотрим два случая: когда (корни совпадают) и когда (корни различные):

• :

  

  При получим

  

  Т.е. система имеет ровно одно решение.

• :

  

  При положительном дискриминанте уравнение имеет два различных отрицательных корня и . При этом выполнено .

  Если , то оба корня лежат на отрезке , т.е. система имеет два различных решения, что нам не подходит. Тогда , т.е.

  

  Если , то оба корня не принадлежат отрезку , т.е. система не имеет решений, что нам также не подходит. Тогда , т.е.

  

  Получили, что в случае решение будет единственным на отрезке при

Тогда исходная система имеет ровно одно решение на отрезке при

Ответ: