18.22 Графика. Нахождение касательной к графику
Ошибка.
Попробуйте повторить позже
При каких значениях параметра уравнение
имеет ровно два решения?
В левой части имеем параболу Правой части соответствует семейство уголков модуля с вершинами на оси ординат, так
как координаты вершины
![]()
Рассмотрим случаи расположения уголка относительно параболы.
- В положении
вершина уголка совпадает с началом координат, то есть
и уголок имеет три точки пересечения с параболой. Этот случай нам не подходит.
- Если вершина уголка находится выше положения
уголок имеет ровно две точки пересечения с параболой: левая ветвь уголка с левой ветвью параболы и правая ветвь уголка с правой ветвью параболы. Этот случай нам подходит.
- Между положениями
и
каждая из ветвей уголка имеет ровно две точки пересечения с соответствующей ветвью параболы, суммарно четыре точки пересечения. Этот случай нам не подходит.
-
Если вершина уголка находится в положении
ветви уголка касаются параболы. Этот случай нам подходит, так как уголок имеет ровно две точки пересечения с параболой.
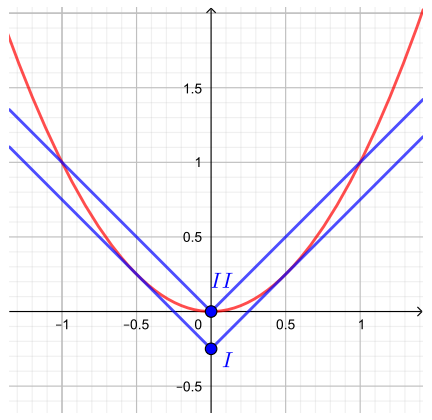
Найдем координаты вершины уголка в положении
В этом положении правая ветвь уголка, которая описывается уравнением
касается параболы, тогда из симметрии картинки и левая ветвь тоже касается. Запишем критерий касания функций
и
чтобы найти
- Если вершина уголка находится ниже положения
то уголок не имеет точек пересечения с параболой. Этот случай нам не подходит.
Объединяя все подходящие получаем
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Ответ может отличаться от верного
включением | 3 |
| ИЛИ | |
| Недостаточное обоснование построения | |
| Рассмотрено верно одно из двух взаимных
расположений графиков функций, при
этом найдено хотя бы одно из ключевых
значений параметра | 2 |
| ИЛИ | |
| Значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков функций | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




