18.21 Графика. Нахождение касательной к графику

Перепишем неравенство в виде:

Пусть , – функции. Тогда по условию задачи необходимо, чтобы промежуток, для которого график лежит не выше графика , содержал ровно одну целую точку.

Заметим, что графиком функции является уголок, вершина которого скользит по прямой . Правая ветвь уголка задается уравнением при ; левая ветвь — при .
 

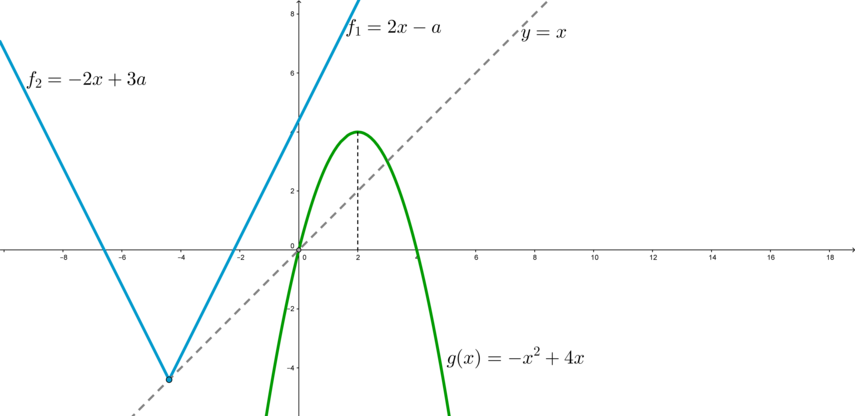
1) Найдем значение параметра, при котором правая ветвь уголка касается параболы (т.к. если уголок находится левее этого положения, то неравенство не имеет решений).
. Если касается в точке , то равно коэффициенту при в уравнении , то есть:

Т.к. касается , то , откуда находим значение параметра .

Таким образом, при правая ветвь касается параболы:
 

Заметим, что при существует ровно одно решение для неравенства, и это , что является целочисленным значением. Следовательно, нам подходит.

2) Заметим, что при вершина уголка находится в точке и уголок имеет две точки пересечения с параболой: и . Следовательно, решением неравенства является отрезок (т.к. на этом отрезке уголок находится не выше параболы), содержащий три целых точки ( и ). А вот при (но ) левая ветвь уголка не пересекает параболу, а правая ветвь пересекает параболу в двух точках, причем одна находится между и , а вторая между и . То есть в промежуток, удовлетворяющий неравенству, будет входить ровно одна целая точка . Следовательно, все нам подходят.
 

3) Заметим, что если вершина уголка находится в точке (то есть ), то левая ветвь уголка касается параболы (в этой точке). Действительно, это можно проверить, поступив так же, как мы поступили в первом пункте: . Если касается в точке , то равно коэффициенту при в уравнении , то есть:

Следовательно, при решением неравенства является единственная точка , которая является целой, то есть нам подходит.

Заметим также, что при уголок будет находится всегда выше параболы, то есть неравенство не будет иметь решений.

4) Рассмотрим ситуацию, когда . При этих правая ветвь уголка пересекает параболу в точке , а вот левая ветвь пересекает параболу в какой-то точке . Следовательно, чтобы неравенство имело единственное целочисленное решение, этим решением должно быть и точка , в которой левая ветвь пересекает параболу, должна удовлетворять: (оранжевый уголок).
 

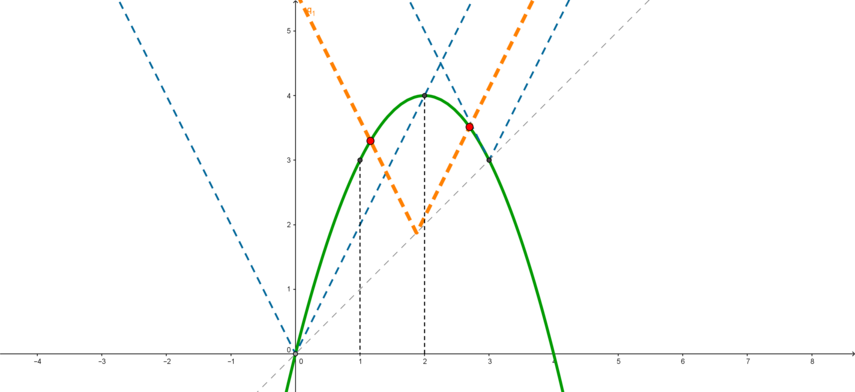
Поэтому найдем значение , при котором левая ветвь уголка пересекает параболу в точке :

Теперь найдем значение , при котором левая ветвь уголка пересекает параболу в точке :

То есть при решением неравенства является отрезок , содержащий 2 целые точки (); при решением неравенства является отрезок , содержащий одну целую точку ().

Следовательно, при решением будет отрезок , который содержит одну целую точку . Такие значения нам подходят.

Таким образом, итоговый ответ:
при целочисленное решение ;
при целочисленное решение ;
при целочисленное решение .