18.22 Графика. Нахождение касательной к графику
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых система уравнений
имеет единственное решение.
Рассмотрим систему внимательнее и преобразуем её условия:
|
|
|
|
|
|
|
|
Получили полуокружность и пучок прямых, проходящих через точку
Перейдём на координатную плоскость
1 случай:

При прямая
становится параллельной оси абсцисс и
проходит ровно через одну точку
полуокружности. Иными словами,
касается полуокружности – такой случай нам подходит и
– часть
ответа.
2 случай:
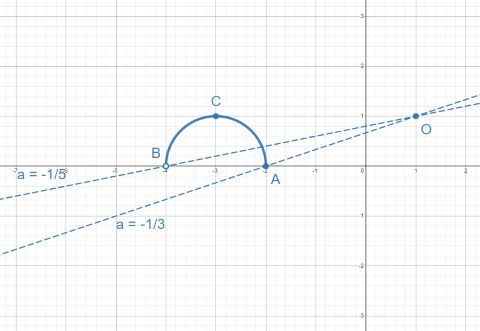
Когда прямая
пересекает полуокружность ровно в
одной точке. Иными словами, мы берём в ответ все прямые, лежащие между
прямыми
и
, включая
и исключая
.
пересекает
полуокружность уже в двух точках.
Вычисления ключевых значений параметра:
Прямая (проходит через точку
):
Прямая (проходит через точку
):
Прямая (проходит через точку
):
.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены все верные значения параметра, но решение недостаточно обосновано | 3 |
| ИЛИ | |
| в ответ включена точка | |
| ИЛИ | |
| потеряна точка | |
| ИЛИ | |
| потеряна точка | |
| С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом верно выполнены все шаги решения | 2 |
| ИЛИ | |
| полученный
ответ отличается от правильного
включением/исключением двух или
трёх точек из набора | |
| В случае аналитического решения
найдено значение | 1 |
| ИЛИ | |
| в случае графического решения: задача верно сведена к исследованию взаимного расположения линий (изображены необходимые фигуры, учтены ограничения, указана связь исходной задачи с построенными фигурами) | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




