18.26 Графика. Отрезок, ромб, квадрат и другие нестандартные графики
Ошибка.
Попробуйте повторить позже
Найдите значения параметра , при которых система
имеет ровно три решения.
Красивое решение
Построим на координатной плоскости множество решений уравнения
— квадрат с вершинами в точках
,
,
и
![]()
График функции — это парабола с вершиной в точке с
координатами
. Заметим, что и квадрат, и парабола симметричны
относительно оси ординат, следовательно, множество точек их пересечения также
симметрично относительно оси ординат. Нам нужно найти такое значение
параметра
, при котором это множество содержит ровно три точки. Три —
нечётное число, значит, хотя бы одна из точек пересечения должна лежать на оси
ординат (ведь если бы не лежало ни одной, то из соображений симметрии точек
было бы четное число).
Квадрат пересекает ось ординат только в двух точках — и
. Парабола
может проходить через них только тогда, когда одна из точек
или
является её вершиной. Значит, достаточно рассмотреть только эти два
случая.
- Если
— вершина параболы, то
Но тогда
. Значит, точка
— единственная точка пересечения параболы и квадрата.
- Если
— вершина параболы, то
. Тогда
. Значит, ветви этой параболы проходят через точки
и
. Больше точек пересечения нет, поэтому парабола
нам подходит.
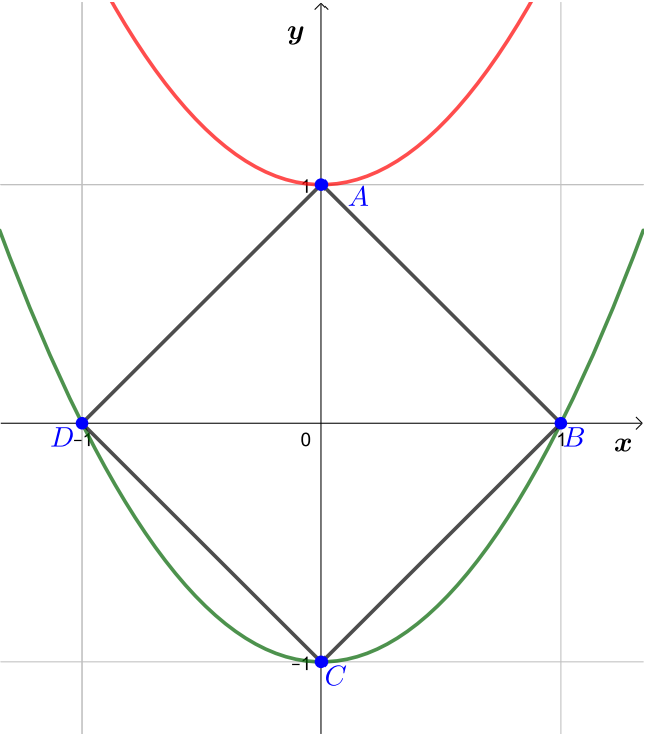
Мы выяснили, что другие параболы будут пересекать квадратик в чётном числе
точек, поэтому ответ — .
Стандартное решение
Построим на координатной плоскости множество решений уравнения
— квадрат с вершинами в точках
,
,
и
![]()
Будем анализировать, как выглядит график функции в
зависимости от значения
. Это парабола с вершиной в точке с координатами
. Заметим, что при
график функции
проходит через
точки
,
и
. Тогда при
этот график не пересекает квадрат ни в
одной точке.
![]()
Если мы начнем уменьшать то график начнёт двигаться вверх, пересекая
каждый из отрезков
и
в двух точках, а каждый из отрезков
и
в одной. То есть у нас будет 6 точек пересечения графика
с квадратом.
Так будет до тех пор, пока график
не достигнет положения касания с
отрезками
и
. В этот момент он будет пересекать каждый из отрезков
и
в одной точке. То есть у нас будет 4 точки пересечения графика
с квадратом.
После этого момента до момента, когда станет равно
, график
будет пересекать отрезки
и
ровно по одному разу. В момент
график
будет проходить только через точку
квадрата. При
график
и квадратик пересекаться не будут. Значит, единственное
подходящее
.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получено верное значение параметра, но есть недостаток в обосновании | 3 |
| Верно рассмотрены ключевые положения квадрата и параболы, но верное значение параметра либо не найдено, либо получены посторонние значения | 2 |
| Обоснованно сведено к исследованию графически или аналитически | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




