18.26 Графика. Отрезок, ромб, квадрат и другие нестандартные графики

Второе уравнение системы задает окружность с центром в точке и радиусом 1.

Напомним, что расстояние между точками и на плоскости задается выражением

Рассмотрим первое уравнение системы. Первое слагаемое левой части равно расстоянию между точками и Второе слагаемое левой части равно расстоянию между точками и Выражение в правой части уравнения равно расстоянию между точками и

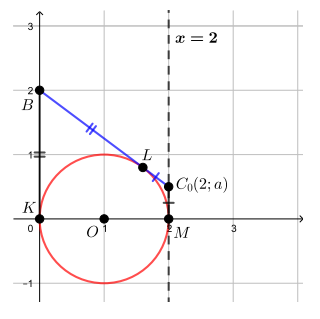
Получили, что первое уравнение системы равносильно тому, что длина отрезка (правая часть) равна сумме длин отрезков и (левая часть). По неравенству треугольника такое возможно только при условии, что точка лежит на отрезке Точка зафиксирована, а точка может лежать в любом месте прямой в зависимости от значения параметра Теперь можем нарисовать картинку.

Отметим ключевое для нас положение точки на прямой В этом положении отрезок касается окружности, то есть имеет с ней единственную точку пересечения.

Если будет лежать выше, чем то отрезок не будет иметь общих точек с окружностью. Если же будет лежать ниже, чем то отрезок будет иметь ровно две точки пересечения с окружностью. Нас интересует последний случай. Осталось найти координаты точки

Обозначим точку через точку касания с окружностью через точку через

как отрезки касательных к окружности из точки и как отрезки касательных к окружности из точки Тогда Выразив длину отрезка через координаты его концов, получим уравнение

Так как отрезок имеет два пересечения с окружностью при всех положениях ниже, чем то нам подойдут значения параметра