18.25 Графика. Отрезок, ромб, квадрат и другие нестандартные графики

1 способ.

 

Рассмотрим .
Тогда уравнение примет вид . Тогда нам нужно найти наименьшее значение , при котором прямая будет пересекать график хотя бы в одной точке. Исследуем . Для этого найдем сначала ее производную:

Найдем нули производной:

Определим знаки производной:
 

Следовательно, схематично график функции выглядит так:
 

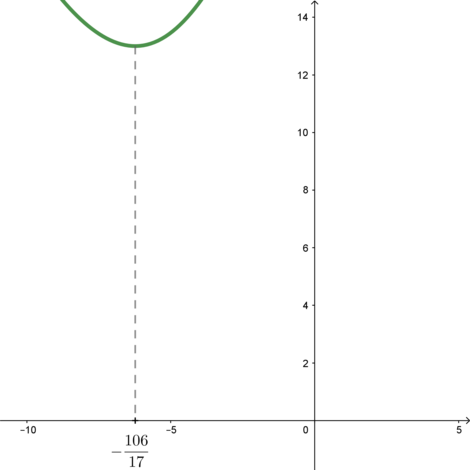
Следовательно, наименьшее значение параметра – когда прямая проходит через точку экстремума функции :

2 способ.

 

Заметим, что в первом способе было очень много вычислений и на самом деле нам повезло, что при решении уравнения слагаемые с и взаимно уничтожились и мы пришли к квадратному уравнению. А что делать, если числа так хорошо не подобраны и мы не получим в конечном итоге “красивое” уравнение, которое сможем решить?
Давайте рассмотрим второй способ решения подобных уравнений.

 

Рассмотрим три точки: , , . Тогда уравнение примет вид

Если нам нужно найти наименьшее значение параметра , при котором уравнение имеет хотя бы одно решение, то нам нужно найти точку , при которой сумма длин отрезков и будет наименьшей.
Где располагается точка ? Эта точка “бегает” по прямой . Графически это выглядит так:
 

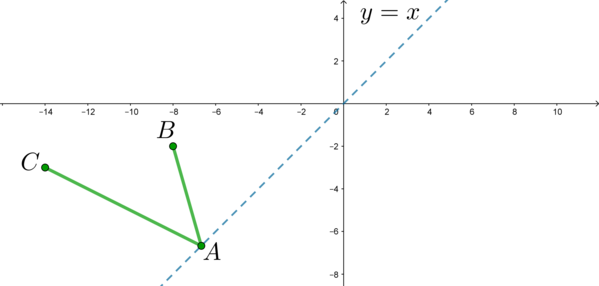
Здесь мы будем использовать классическую идею планиметрии. Отразим симметрично точку относительно прямой (то есть проведем , где :
 

Тогда . Заметим, что по правилу треугольника, если точка не лежит на отрезке , то . Следовательно, наименьшая сумма длин будет достигаться тогда, когда .
 

Таким образом, мы идейно поняли, где должна находиться точка . Теперь осталось найти ее координаты.

 

1) Найдем координаты точки .
Для этого сначала найдем уравнение прямой . Так как , то если уравнение прямой имеет вид , то (произведение угловых коэффициентов двух взаимно перпендикулярных прямых равно ). Следовательно, .
Для того, чтобы найти число , нужно подставить координаты точки в уравнение прямой:

Следовательно, уравнение прямой имеет вид .
Найдем координаты точки – это точка пересечения прямых и : – середина отрезка . Значит, если координаты точки равны , то Таким образом, .

 

2) Найдем уравнение прямой . Если уравнение этой прямой в общем виде выглядит как , то

Следовательно, . Теперь можно найти координаты точки – это точка пересечения прямых и :

3) Теперь можно найти значение параметра .

Чем хорош этот способ? Во-первых, он более изящный. Во-вторых, в ходе решения мы сталкивались только с линейными уравнениями, которые решать намного проще.