18.18 Функции. Исследование функции на возрастание/убывание

Сделаем замену для удобства: . Тогда неравенство примет вид:

Сделав обратную замену и учитывая, что , получим:

Преобразуем функцию, максимальное значение которой нужно найти:

Таким образом, функция примет вид:

Таким образом, графиком функции при каждом фиксированном значении является парабола, ветви которой направлены вниз, а вершина параболы находится в точке :
 

 

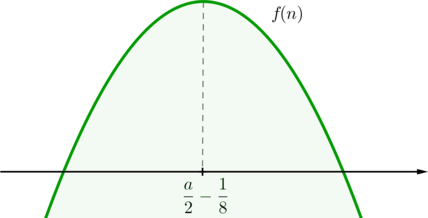
Рассмотрим параболу только при целых (так как, вообще говоря, – целое). ни при каких целых не будет являться целым числом. Следовательно, наибольшее значение функция принимает точно не в вершине.

 

Рассмотрим два случая:

 

1) .

 

Тогда . Следовательно, парабола выглядит так:
 

 

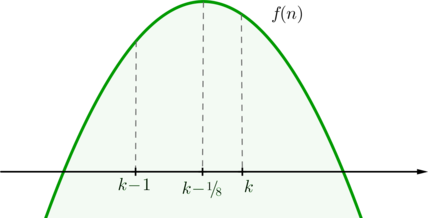
Заметим, что так как парабола симметрична относительно прямой , то чем ближе число расположено к , тем больше будет значение функции в нем. Следовательно, максимальное значение функция будет принимать либо при , либо при . Заметим, что находится ближе к , чем . Таким образом:

2) .

 

Тогда . Следовательно, парабола выглядит так:
 

 

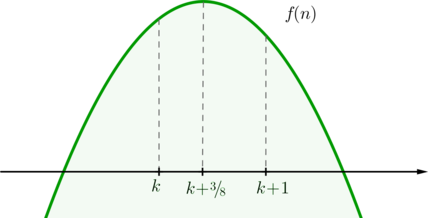
Аналогично, максимальное значение функция будет принимать либо при , либо при . Заметим, что находится ближе к , чем . Таким образом: