Законы сохранения в механике —Каталог задач по ЕГЭ - Физика

Ошибка.
Попробуйте повторить позже

Задача 1#14398

Два шарика массами $m1 = 0,01$ кг и $m2 = 0,02$ кг движутся навстречу друг к другу с одинаковыми скоростями равными $v = 0,5$ м/с. Найти скорость шариков после абсолютно неупругого столкновения.

Источники: Основная волна 2020

Показать ответ и решение

Закон сохранения импульса выглядит следующим образом

⃗p1+ ⃗p2 = ⃗p′,

где $p1$ и $p2$ – импульсы шариков до столкновения, $′ p$ – импульс системы после столкновения.
Так как шарики сталкиваются неупруго, то они движутся как одно целое. Импульс находится по формуле:

p= mv,

где $m$ – масса тела, $v$ – его скорость.
Запишем закон сохранения импульса, выбрав за положительную ось направление движения второго шарика:

m2v − m1v = (m1+ m2)u ⇒ u= v(m2-−-m1) m2+ m1

u= 0,5-м/с(0,02 кг−-0,01 кг)≈ 0,17 м/с 0,02 кг+ 0,01 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения импульса, формула импульса);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 2#14399

Камень массой $√- m1 = 3 3$ кг бросают вертикально вверх с начальной скоростью $v0 = 50$ м/с, после трех секунд полета в него влетает снаряд массой $m2 = 0,3$ кг летящий горизонтально со скоростью $v2 = 200$ м/c, и застревает в нем. Найдите угол отклонения от первоначальной траектории полета камня.

Показать ответ и решение

Сделаем рисунок системы "камень+снаряд"после столкновения.

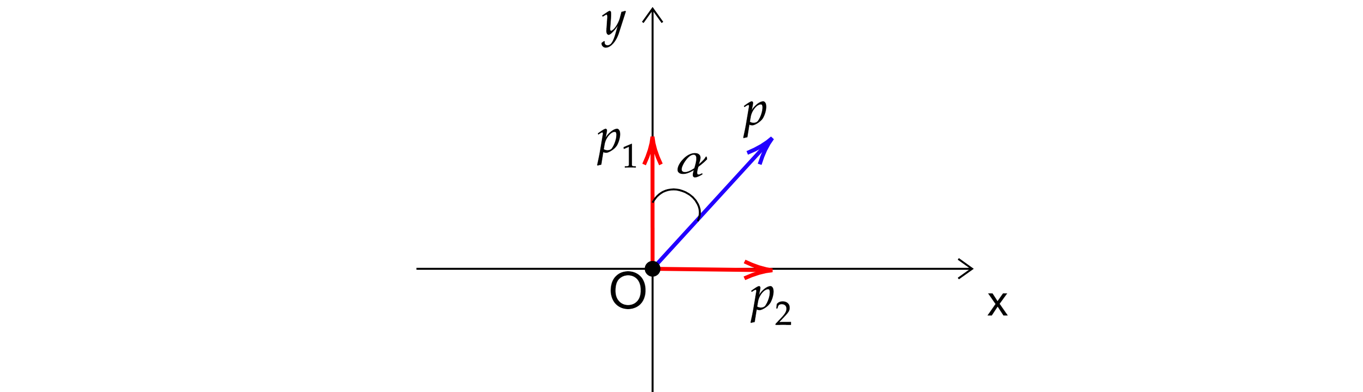
Где $p1$ – импульс камня до столкновения, $p2$ – импульс снаряда до столкновения, О – точка столкновения камня и снаряда, $p$ – суммарный импульс системы после столкновения, а угол $α$ – угол отклонения от первоначальной траектории.

Камень, летящий вверх, движется равнозамедленно. Найдем скорость камня в момент столкновения по формуле:

v1 = v0− gt

Где $t$ – время полета камня. Скорость камня в момент столкновения равна

v = 50 м/с− 10 м/c2⋅3 с= 20 м/c 1

Так как система замкнутая, то выполняется закон сохранения импульса.

p⃗ +p⃗= ⃗p 1 2

Импульсы тел до столкновения найдем по формулам: $p1 = m1v1$ и $p2 = m2v2$

Тогда $p = 3√3-кг⋅ 20 м/c =60√3-кг-м 1 с$ , а $p = 0,3кг ⋅200 м/c= 60 кг-м 2 с$

Спроецируем закон сохранения импульса на оси $Oy$ и $Ox$ и запишем полученные уравнения

({ Ox : p1 = pcosα (Oy : p2 = psinα

Выразим $p$ из каждого уравнения

(| p1 {Ox : p = cosα- (1) |(Oy : p = -p2- (2) sinα

Приравняем (1) и (2)

-p1-= -p2-⇒ p1sinα = p2cosα cosα sin α

√- 60 3sin α= 60cosα

Поделим уравнение на $60 cosα$

√ - 1 3tgα = 1⇒ tgα = √-- 3

Следовательно, угол отклонения составил 30 градусов

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: уравнение кинематики для описания изменения скорости при движении в поле силы тяжести, закон сохранения импульса, формула импульса тела);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 3#14400

Камень массой $√- m1 = 3 3$ кг бросают вертикально вверх с начальной скоростью $v0 = 50$ м/с, после трех секунд полета в него влетает снаряд массой $m2 = 0,3$ кг, летящий горизонтально со скоростью $v2 = 200$ м/c, и застревает в нем. Найдите импульс системы "камень+снаряд"после столкновения.

Показать ответ и решение

Сделаем рисунок системы "камень+снаряд"после столкновения.

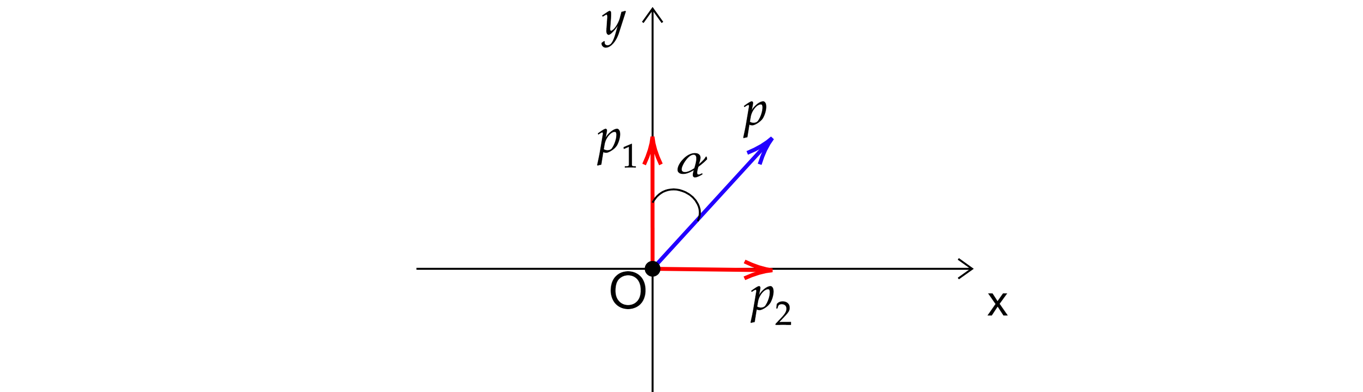
Где $p1$ – импульс камня до столкновения, $p2$ – импульс снаряда до столкновения, О – точка столкновения камня и снаряда, $p$ – суммарный импульс системы после столкновения, а угол $α$ – угол отклонения от первоначальной траектории.

Камень, летящий вверх, движется равнозамедленно. Найдем скорость камня в момент столкновения по формуле:

v1 = v0− gt

Где $t$ – время полета камня. Скорость камня в момент столкновения равна

v = 50 м/с− 10 м/c2⋅3 с= 20 м/c 1

Так как система замкнутая, то выполняется закон сохранения импульса.

p⃗ +p⃗= ⃗p 1 2

Импульсы тел до столкновения найдем по формулам: $p1 = m1v1$ и $p2 = m2v2$

Тогда $p =3√3-кг⋅20 м/c= 60√3-кг м 1 с$ , а $p = 0,3кг⋅200 м/c= 60-кг м 2 с$ По теореме Пифагора можно найти $p$

∘ ------ p= p21+ p22 = 120 кг-м- с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: уравнение кинематики для описания изменения скорости при движении в поле силы тяжести, закон сохранения импульса, формула импульса тела);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 4#14401

Камень массой $m = 2$ кг брошен с высоты $H = 25$ м под углом к горизонту с начальной скоростью $v0 = 10$ м/c $2$ . Найдите кинетическую энергию камня на высоте $h = 10$ м.

Показать ответ и решение

По закону сохранения энергии:

Eпот1 +E кин1 = Eпот2+E кин2

Где $E пот1$ – потенциальная энергия на высоте $H$ , $Eкин1$ – кинетическая энергия на высоте $H$ , $Eпот2$ – потенциальная энергия на высоте $h$ , а $E кин2$ – кинетическая энергия на высоте $h$ . Выразим $Eкин2$

Eкин2 = Eпот1+ Eкин1− Eпот2 (1)

Найдем потенциальную энергию на высоте $H$ по формуле:

Eпот1 = mgH (2)

А кинетическую энергию на высоте $H$ по формуле:

mv20 Eкин1 = -2-- (3)

Потенциальная энергия на высоте $h$ находится по формуле:

Eпот2 =mgh (4)

Подставим формулы (2), (3) и (4) в (1)

mv20- v20 100 м2/c2 Eкин2 = mgH + 2 +mgh = m (gH + 2 − gh) =2 кг(10 Н/кг⋅25 м + 2 − 10 Н/кг ⋅10 м)= 400 Д ж

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон изменения и сохранения механической энергии, формула кинетической энергии материальной точки, формула потенциальной энергии тела в однородном поле тяжести);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 5#14402

Камень массой $m = 2$ кг брошен с высоты $H = 45$ м под углом к горизонту с начальной скоростью $v0 = 10$ м/c. Найдите импульс камня на высоте $h = 10$ м.

Показать ответ и решение

По закону сохранения энергии:

Eпот1 +E кин1 = Eпот2+E кин2

Где $E пот1$ – потенциальная энергия на высоте $H$ , $Eкин1$ – кинетическая энергия на высоте $H$ , $Eпот2$ – потенциальная энергия на высоте $h$ , $Eкин2$ – кинетическая энергия на высоте $h$ , а $E кин2$ – кинетическая энергия камня на высоте $h$

Eкин2 = Eпот1+ Eкин1− Eпот2 (1)

Найдем потенциальную энергию на высоте $H$ по формуле:

Eпот1 = mgH (2)

А кинетическую энергию на высоте $H$ по формуле:

2 Eкин1 = mv0- (3) 2

Потенциальная энергия на высоте $h$ находится по формуле:

Eпот2 =mgh (4)

А кинетическую энергию на высоте $h$ по формуле:

mv21- Eкин2 = 2 (5)

Подставим формулы (2) (3) (4) в (1)

mv20- v20 100 м2/c2 Eкин2 = mgH + 2 − mgh = m (gH + 2 − gh) =2 кг(10 Н/кг⋅45 м + 2 − 10 Н/кг ⋅10 м)= 800 Д ж

Подставим значение $Eкин2$ в формулу (5)

2 800 Дж = mv-1 2

Выразим скорость тела на высоте $h$

∘ ---- v1 = 1600 (6) m

Импульс тела найдем по формуле:

p= mv 1

Подставим формулу (5) в формулу импульса тела

∘-------- 1600-Дж- √ - √ -кг-м- -кг м p = 2 кг 2 кг = 2 2 кг20 м/c =40 2 с =56,6 с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон изменения и сохранения механической энергии, формула кинетической энергии материальной точки, формула потенциальной энергии тела в однородном поле тяжести, формула импульса материальной точки);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 6#14403

Шарик массой $m = 2$ кг падает с высоты $h = 5$ м, без начальной скорости, в результате его удара об пол выделилась количество теплоты $Q = 20$ Дж. Найдите максимальную высоту подъема шарика после удара о землю.

Показать ответ и решение

Так как шарик падает без начальной скорости, то кинетическая энергия вначале полета равна 0, аналогично с кинетической энергией на максимальной высоте после удара шарика об землю, следовательно, закон сохранения энергии можно переписать в виде:

E пот1 = E пот2+ Q (1)

Где $E пот1$ – потенциальная энергия на высоте $h$ , $E пот2$ – потенциальная энергия на максимальной высоте после удара. Они находятся по формулам:

Eпот1 = mgh (2)

E пот2 =mgH (3)

$H$ – максимальная высота подъема камня после удара о землю. Подставим (2) и (3) в (1)

mgh = mgH + Q

Выразим $H$

mgh − Q H = ---mg---

Подставим числа из условия

H = 2-кг⋅10 Н/кг-⋅5-м−-20-Дж-= 4 м 2 кг ⋅10 Н/кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения энергии с учетом количества теплоты, выделившейся при ударе, формула потенциальной энергии тела в однородном поле тяжести);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 7#14404

Снаряд массой $m = 2 кг$ разрывается на два равных осколка, один летит под углом 90 градусов к первоначальному направлению движения, другой под углом 30 градусов, скорость первого осколка $v1 = 10 м/с.$ Найдите импульс снаряда до разрыва.

Показать ответ и решение

Сделаем рисунок

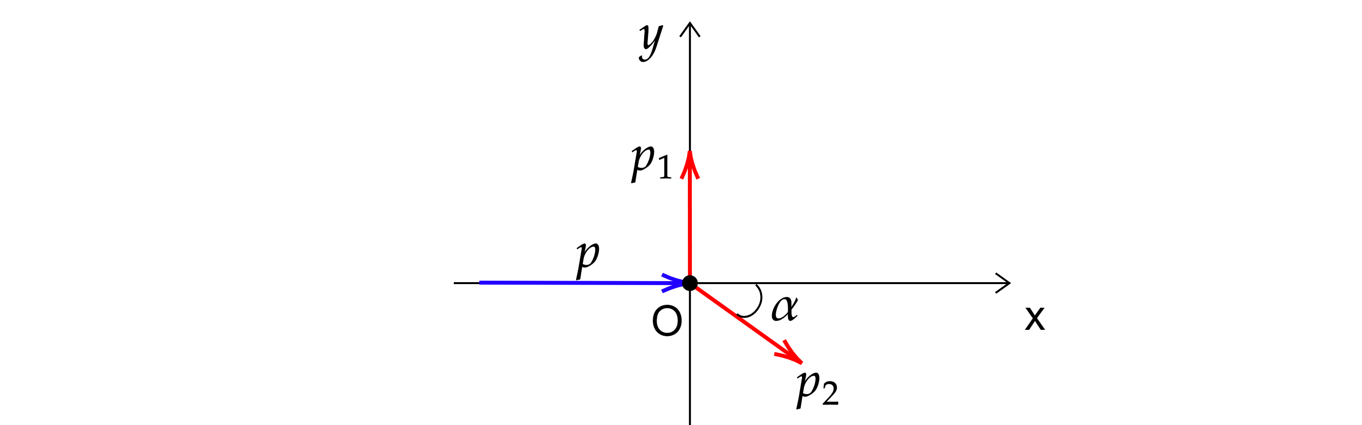
Где $p$ – импульс снаряда, $p1$ – импульс первого осколка, $p2$ – импульс второго осколка.

По закону сохранения импульса

p⃗= ⃗p1+ ⃗p2

Спроецируем закон сохранения импульса на оси $Oy$ и $Ox$ и запишем полученные уравнения

( { Ox : p= p2cosα (1) ( Oy : 0= p1− p2sinα (2)

Выразим из (2) $p2$

p2 =-p1- (3) sin α

Затем подставим (3) в (1)

p = p1-cosα- (4) sinα

Импульс первого осколка массой $m- 2$ находится по формуле:

p1 = mv1 (5) 2

Подставим (5) в (4)

2 кг 10 м/c √3 mv1-cosα -------2--------- кг-м- p= 2sinα = 2 ≈ 17 с 2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения импульса, формула импульса);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 8#14405

Камень массой $m = 2 кг$ брошен под углом $∘ 30 .$ Начальный модуль импульса тела равен $-кг⋅м p0 = 4 с .$ Чему равна кинетическая энергия камня в верхней точке траектории его движения?

Показать ответ и решение

Во время подъема вертикальная составляющая импульса будет уменьшаться, пока не достигнет нуля, а горизонтальная будет неизменна и она находится по формуле:

px = pocos30∘ = px =mv0 cos30∘ (1)

Кинетическая энергия камня в верхней точке находится по формуле:

mv2 m2v2 Ek = -2x-⇒ Ek = 2m-x- (2)

Подставим (1) в (2)

2 2 2 2 2 2 2 2 2 Ek = px-= p0cos-30-= 4кг--м-/c-⋅3-= 48 кг-м-/c-= 3 Дж 2m 2m 4⋅2⋅2 кг 16 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула импульса, формула кинетической энергии);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 9#14406

Шайбе массой $m = 1 кг,$ находящейся на наклонной плоскости, сообщили скорость $v = 4 м/с,$ направленную вверх вдоль наклонной плоскости. Угол наклона плоскости $30∘.$ Какова будет скорость шайбы, после того, как она пройдет $l = 0,5 м,$ если сила трения равна $F = 1 Н.$

Показать ответ и решение

Запишем закон об изменении кинетической энергии

Ek − Ek0 = −En − Q

Где $Ek0$ – кинетическая энергия тела в начале движения, $Ek$ – кинетическая энергия в конце движения $En$ – потенциальная энергия в конце движения, а $Q$ – количество теплоты. Закон сохранения энергии можно переписать в виде

′2 2 mv--− mv--= −mgh − A тр 2 2

Где $h$ – высота поднятия шайбы $h= lsin 30 = 0,25$ м, а $Aтр = F l$ – работа силы трения. Выразим конечную скорость $v′$

┌││ -(-mv2------------)- ┌││--(-1 кг⋅16м2/c2-----------------------------) ′ ││ | -2--−-mgh−-A-тр| ││ |------2-----−-1 кг⋅10-Н/кг⋅0,25-м−-1-Н⋅0,5 м-| v = ∘ 2( m ) = ∘2 ( 1 кг ) = 3,2 м/с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон изменения кинетической энергии, формула кинетической энергии тела, формула потенциальной энергии тела в поле силы тяжести, формула работы силы трения);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 10#14407

Шайбе массой $m = 1$ кг, находящейся на наклонной плоскости, сообщили скорость $v = 4$ м/с, направленную вверх вдоль наклонной плоскости. Угол наклона плоскости $30∘$ . Шайба остановилась на расстоянии $S = 1$ м от начала движения. Чему равна сила трения шайбы о плоскость?

Показать ответ и решение

Запишем закон об изменении кинетической энергии

0− Ek = −En − Q

Где $Ek$ – кинетическая энергия тела в начале движения, $En$ – потенциальная энергия в конце движения, а $Q$ – количество теплоты. Закон сохранения энергии можно переписать в виде

mv2 0− --2-= − mgh− A тр

Где $h$ – высота поднятия шайбы $h= lsin30 = 0,5$ , а $A тр$ – работа силы трения. Работа силы трения равна $A тр = F трS (1)$ Выразим силу трения с учетом (1)

F тр = mv2−-2mgh-= 1-кг--16-м2/c2−-1-кг--10-кг/Н--- = 3 Н 2S 2 1 м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон изменения кинетической энергии, формула кинетической энергии тела, формула потенциальной энергии тела в поле силы тяжести, формула работы силы трения);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 11#14408

Шар массой $m1 =5$ кг со скоростью $v1 = 3$ м/с врезается в неподвижный шар массой $m2 = 10$ кг. В результате их упругого столкновения второй шар приобрел скорость, а первый отскочил в обратном направлении. Найдите кинетическую энергию первого шара после столкновения.

Показать ответ и решение

Запишем систему, состоящую из закона сохранения импульса и закона сохранения энергии

( {p⃗1 = ⃗pk1+ p⃗k2 (E1 = Ek1+ Ek2

Запишем систему с учетом проекций векторов

( {p1 =− pk1 +pk2 (E1 = Ek1+ Ek2

Где $p1$ и $E1$ – импульс и кинетическая энергия первого шара до столкновения, $pk1$ и $Ek1$ – импульс и кинетическая энергия первого шара после столкновения, а $pk2$ и $Ek2$ – импульс и кинетическая энергия второго шара после столкновения. Импульс находится по формуле:

p= mv (1)

А кинетическая энергия тела:

mv2 E = -2-- (2)

Подставим (1) и (2) в систему с учетом индексов

( |{ m1v1 = − m1vk1+ m2vk2 m1v2 m1v2 m2v2 |( --21-= --2k1+ --2-k2

Умножим на 2 второе уравнение

({ m1v1 = − m1vk1+ m2vk2 ( m1v21 = m1v2k1 +m2v2k2

Перенесем с $m1$ в одну сторону, а с $m2$ в другую и вынесем массы за скобку

({ m1(v1+ vk1) =m2vk2 (m1(v21 − v2k1) =m2v2k2

Во втором уравнении преобразуем разность квадратов

( { m1(v1+vk1)= m2vk2 (1) ( m1((v1− vk1)(v1+ vk1))= m2v2k2 (2)

Поделим (2) на (1)

2 m1((v1−-vk1)(v1+-vk1))= m2v-k2 ⇒ vk2 = v1− vk1 (3) m1 (v1+ vk1) m2vk2

Подставим (3) в (1) и выразим $v k1$

v1(m1 − m2) m1(v1+ vk1)= m2(v1− vk1) ⇒ vk1 = -m2-+-m1-- (4)

Подставим (4) в формулу для нахождения кинетической энергии первого шара после столкновения

m1v2(m2 − m1)2 5 кг 9 м2/c2 (10 кг− 5 кг)2 Ek1 =--2(m12-+-m1)2--= ------2(10-кг+-5 кг)2-----= 2,5 Дж

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения импульса в векторной форме и в проекции на координатную ось, закон изменения и сохранения механической энергии, формула импульса материальной точки, формула кинетической энергии материальной точки);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 12#14409

Шар начал падать с некоторой высоты без начальной скорости. Пролетев 50 м, шар приобрел скорость 20 м/с. Найдите чему равно отношение изменения потенциальной энергии к работе сопротивления воздуха.

Показать ответ и решение

Запишем закон сохранения энергии

Ek0 +En0 = Ek + En + A,

где $Ek0$ – кинетическая энергия тела в начале движения, $Ek$ – кинетическая энергия тела в конце движения, $En0$ – потенциальная энергия в начале движения $En$ – потенциальная энергия в конце движения, а $A$ – работа сопротивления воздуха.
Пусть начальный уровень ( $h= 0$ ) конечная точка пути, тогда конечная потенциальная энергия равна нулю, и начальная кинетическая тоже, так как начальная скорость равна нулю. Тогда закон сохранения энергии перепишем в виде.

En0 = Ek + A

Или

mv2- mgh = 2 + A

Отсюда работа сопротивления воздуха

2 A = mgh − mv-- 2

А изменение потенциальной энергии

ΔE = 0− mgh =− mgh

Найдем искомое отношение

ΔE- = --−-mgh---= -----10-Н/кг⋅50 м-----≈ 1,67 A mgh − mv2- 10 Н/кг⋅50 м − 400-м2/c2 2 2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения механической энергии, формула потенциальной энергии в поле силы тяжести, формула кинетической энергии, выражена работа сопротивления воздуха, расписано изменение потенциальной энергии в поле силы тяжести);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 13#14410

При разрыве нити, удерживающей пружину в сжатом на 1 см состоянии (см. рисунок), шарик приобретает скорость 10 м/с. Жесткость пружины 2кН/м. Какова масса шарика. Колебаниями пружины после отрыва шарика пренебречь.

Показать ответ и решение

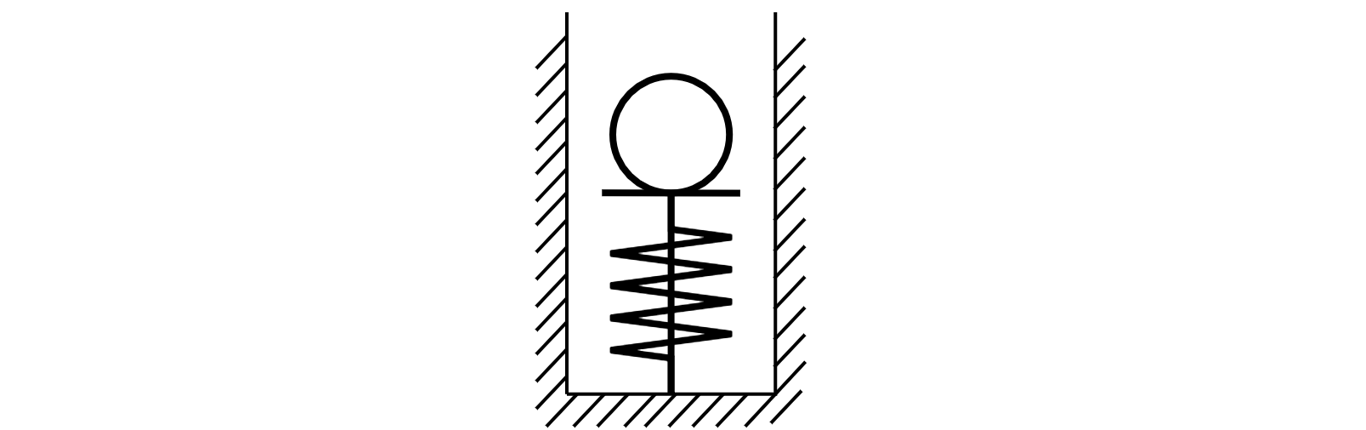
При разрыве нити потенциальная энергия пружины переходит в кинетическую энергию мяча.
По закону сохранения энергии:

kx2 mv2 -2- = -2--

где $2 kx- 2$ – потенциальная энергия деформированной пружины, $2 mv-- 2$ – кинетическая энергия мяча, $k$ – жесткость пружины, $x$ – сжатие, $m$ – масса шарика, $v$ – скорость шарика.
Отсюда масса шарика

kx2 2⋅103 Н/м-⋅10−-4 м2 −3 m = v2 = 102 м2/с2 = 2⋅10 кг= 0,002 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула потенциальной энергии деформированной пружины, формула кинетической энергии, закон сохранения энергии);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 14#14411

Человек на санках, общей массой 100 кг, спустился с ледяной горы высотой 6 м. Сила трения при его движении по горизонтальной поверхности равна 160 Н. Какое расстояние проехал он по горизонтали до остановки? Считать, что по склону горы санки скользили без трения.

Источники: Демидова 2019

Показать ответ и решение

Потенциальная энергия на высоте $h = 6$ м перейдет в кинетическую энергию у подножья горки, которая впоследствии перейдет в работу сил трения, то есть

En = Ek = A

Или

mgh = FS

где $m$ – масса человека и санок, $F$ – сила трения, $S$ – расстояние движения по горизонтали.
Откуда $S$ равно

S = mghF = 100-кг⋅11060 Н/Н-кг⋅6 м-= 37,5 м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон изменения и сохранения механической энергии, формула работы силы при перемещении тела, формула потенциальной энергии);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 15#14412

Тело массой 2 кг бросили вертикально вверх с некоторой высоты, при падении на землю тело имело скорость 6 м/с. Потенциальная энергия в момент броска равна 32 Дж. С какой начальной скоростью бросили тело? Сопротивлением воздуха пренебречь.

Показать ответ и решение

Кинетическая энергия находится по формуле:

mu2 Ek = -2--,

где $m$ – масса тела, $u$ – его скорость
Пусть тело бросили с начальной скоростью $v0$ , а конечная скорость равна $v$ , тогда выполняется закон сохранения энергии, при этом вся потенциальная энергия тела перейдет в кинетическую.

E + mv20= mv2- n 2 2

где $m$ – масса тела, $En$ – начальная потенциальная энергия тела.
Отсюда начальная скорость

∘-------- ∘ ----------------- v0 = v2− 2En-= 36 м2/с2− 2⋅32-Дж-= 2 м/с m 2 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула кинетической энергии, закон сохранения энергии);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 16#14425

Шарик на длинной лёгкой нерастяжимой нити совершает колебания. Максимальная потенциальная энергия шарика в поле тяжести, если считать её равной нулю в положении равновесия, равна 0,8 Дж. Максимальная скорость шарика в процессе колебаний равна 2 м/с. Какова масса шарика? Сопротивлением воздуха пренебречь.

Показать ответ и решение

Так как сопротивлением воздуха пренебречь, то вся потенциальная энергия перейдет в кинетическую, то есть

mv2 E = -2--= 0,8 Дж.

где $m$ – масса шарика, $v$ – его скорость Отсюда масса шарика

m = 1,6-Д2ж- = 1,62Дж2 = 0,4 кг v 4 м /с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения механической энергии, формула кинетической энергии тела);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 17#14426

Груз массой 2 кг, закреплённый на пружине жёсткостью 200 Н/м, совершает гармонические колебания с амплитудой 10 см. Какова максимальная скорость груза?

Показать ответ и решение

Вся потенциальная энергия пружины перейдет в кинетическую, то есть

kx2 mv2 -2- = -2--

где $k$ – жесткость пружины, $x$ – максимальное растяжение пружины, $m$ – масса груза, $v$ – максимальная скорость груза. Найдем скорость груза

∘ --- ∘ -------- v = x k-= 0,1 м 200-Н/м = 1 м/с m 2 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения механической энергии, формула кинетической энергии тела, формула потенциальной энергии деформированной пружины);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 18#14427

Груз массой 2 кг, закреплённый на пружине жесткостью 200 Н/м, совершает горизонтальные гармонические колебания. Максимальное ускорение груза при этом равно 10 м/с $2.$ Какова максимальная скорость груза?

Показать ответ и решение

По второму закону Ньютона

ma 2 кг⋅10 м/с2 F = ma ⇒ kx = ma ⇒ x= k--= --200 Н/м--= 0,1 м

Вся потенциальная энергия пружины перейдет в кинетическую, то есть

kx2 = mv2- 2 2

где $k$ – жесткость пружины, $x$ – максимальное растяжение пружины, $m$ – масса груза, $v$ – максимальная скорость груза. Найдем скорость груза

∘ --- ∘ -------- v = x k-= 0,1 м 200-Н/м = 1 м/с m 2 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: второй закон Ньютона, закон сохранения механической энергии, формула кинетической энергии тела, формула потенциальной энергии деформированной пружины);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 19#18876

Граната, летящая с некоторой скоростью, разрывается на 2 осколка. Первый осколок летит перпендикулярно движению гранаты со скоростью $v1 = 20$ м/с. Второй осколок летит со скоростью $40$ м/с под углом $α= 60∘$ к первоначальной траектории движения. Найдите отношение массы первого осколка к массе второго осколка.

Показать ответ и решение

Спроецируем импульсы осколков на ось, перпендикулярную оси движения гранаты

0= p1− p2sinα

где $p1$ и $p2$ – импульс первого и второго осколков. Распишем импульсы по формуле импульса $p = mv$ и получим

m1v1 =m2v2 sin60∘

Отсюда отношение массы первого к массе второго

m1 v2sin60∘ 40 м/с⋅√3 m2-= --v1---= -2⋅20-м/с = 1,7

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения импульса, формула импульса);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 20#18908

Снаряд, летящий с некоторой скоростью, распадается на два осколка. Скорость большего осколка по величине равна начальной скорости снаряда и направлена перпендикулярно к ней. Скорость другого осколка по величине в 5 раз больше первоначальной. Найдите отношение масс осколков.

Показать ответ и решение

Запишем закон сохранения импульса в векторной форме:

(m1 + m2)⃗v = m1u⃗1 +m2 ⃗u2,

где $m1$ и $m2$ – массы большего и меньшего осколков, $v$ – начальная скорость снаряда, $u1$ и $u2$ – скорости большего и меньшего осколков.

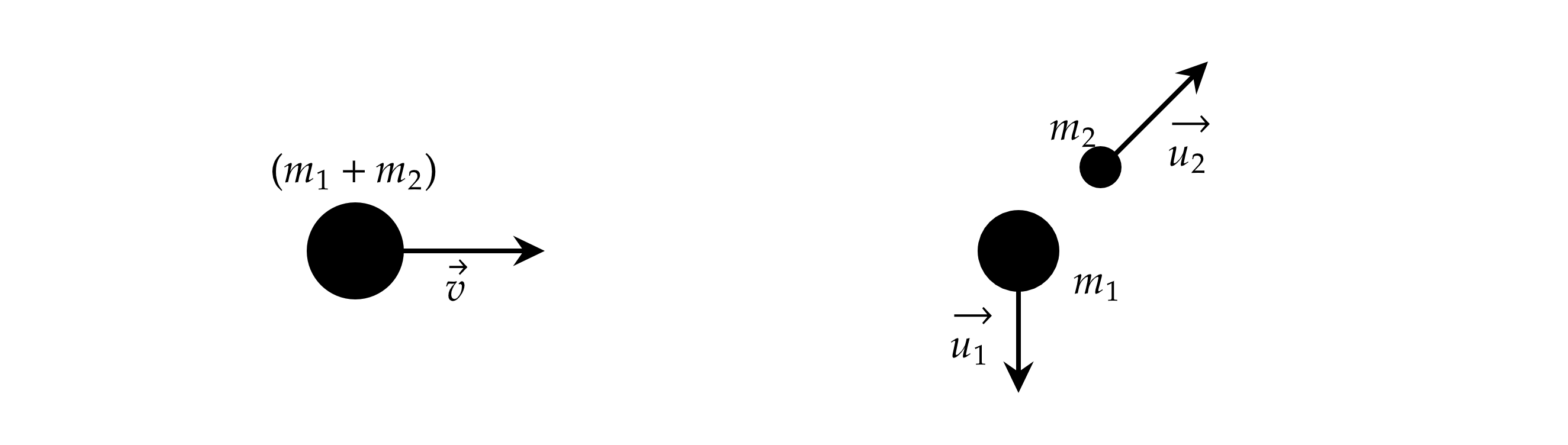
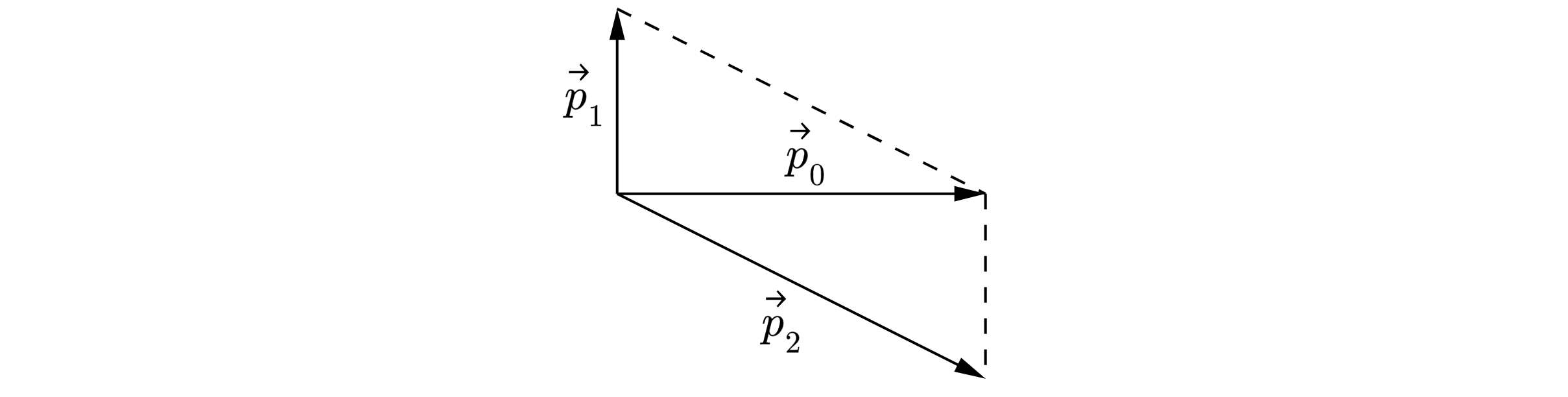
Изобразим закон сохранения импульса на рисунке.

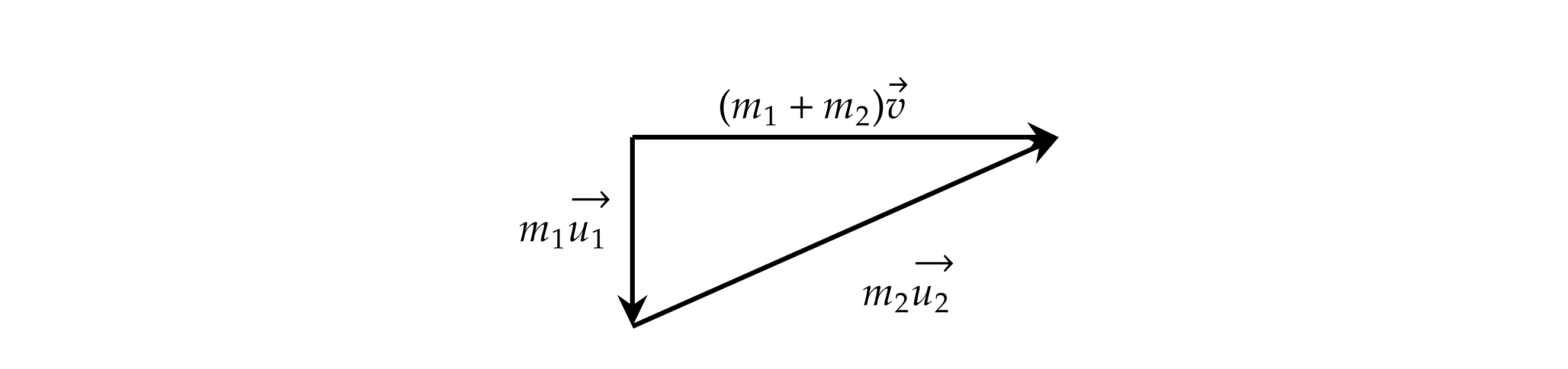
Тогда из векторного треугольника:

(m1+ m2)2v2+ m21u21 = m22u22,

так как по условию $u1 = v$ , $u2 = 5v$ , получаем

m21+ m1m2 − 12m22 = 0.

делим на $2 m2$ и получим квадратное уравнение относительно $x= m1∕m2$

x2+ x− 12= 0.

Находим дискриминант

2 D =1 +48 = 7

−1± 7 x1,2 = --2--. x1 =− 4; x2 = 3.

Отношение масс не может быть отрицательным, значит, в ответ пойдет 3.

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	2
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения импульса, формула импульса);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования,
приводящие к правильному ответу;
IV) представлен правильный ответ

Правильно записаны все необходимые положения теории,	1
физические законы, закономерности, и проведены преобразования,
направленные на решение задачи, но имеется один или несколько
из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения
и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях допущены
ошибки, и (или) в математических преобразованиях пропущены
логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерения величины)

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1 или 2 балла

Максимальный балл	2

05 Законы сохранения в механике