.01 МКТ
Ошибка.
Попробуйте повторить позже
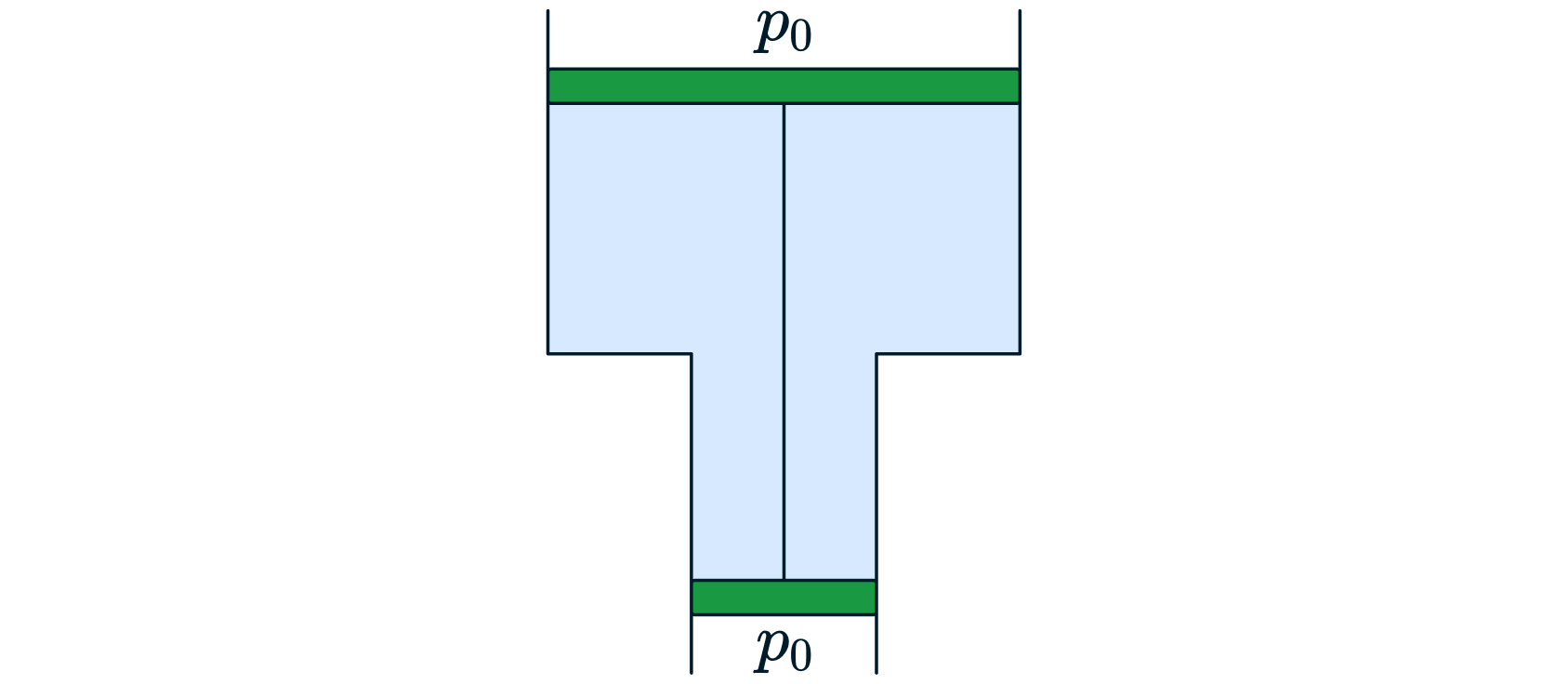
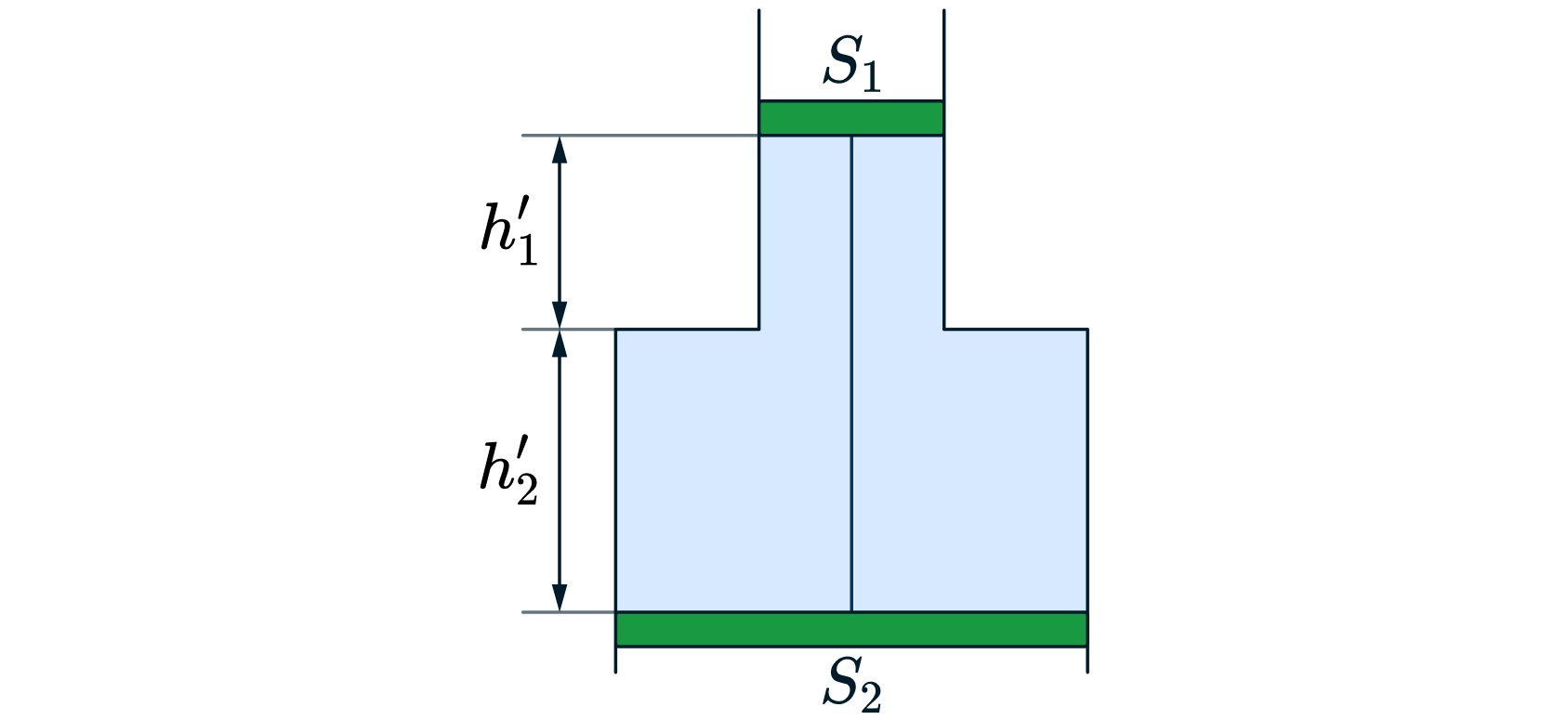
В гладкой, открытой с обоих концов вертикальной трубе, имеющей два разных сечения, находятся два поршня, соединенные
стержнем длиной , а между поршнями
идеального газа. Площадь сечения верхнего поршня
, а нижнего
. Давление газа
, давление наружного воздуха
.
На сколько нужно изменить температуру газа между поршнями, чтобы они переместились вниз на
?
Источники:
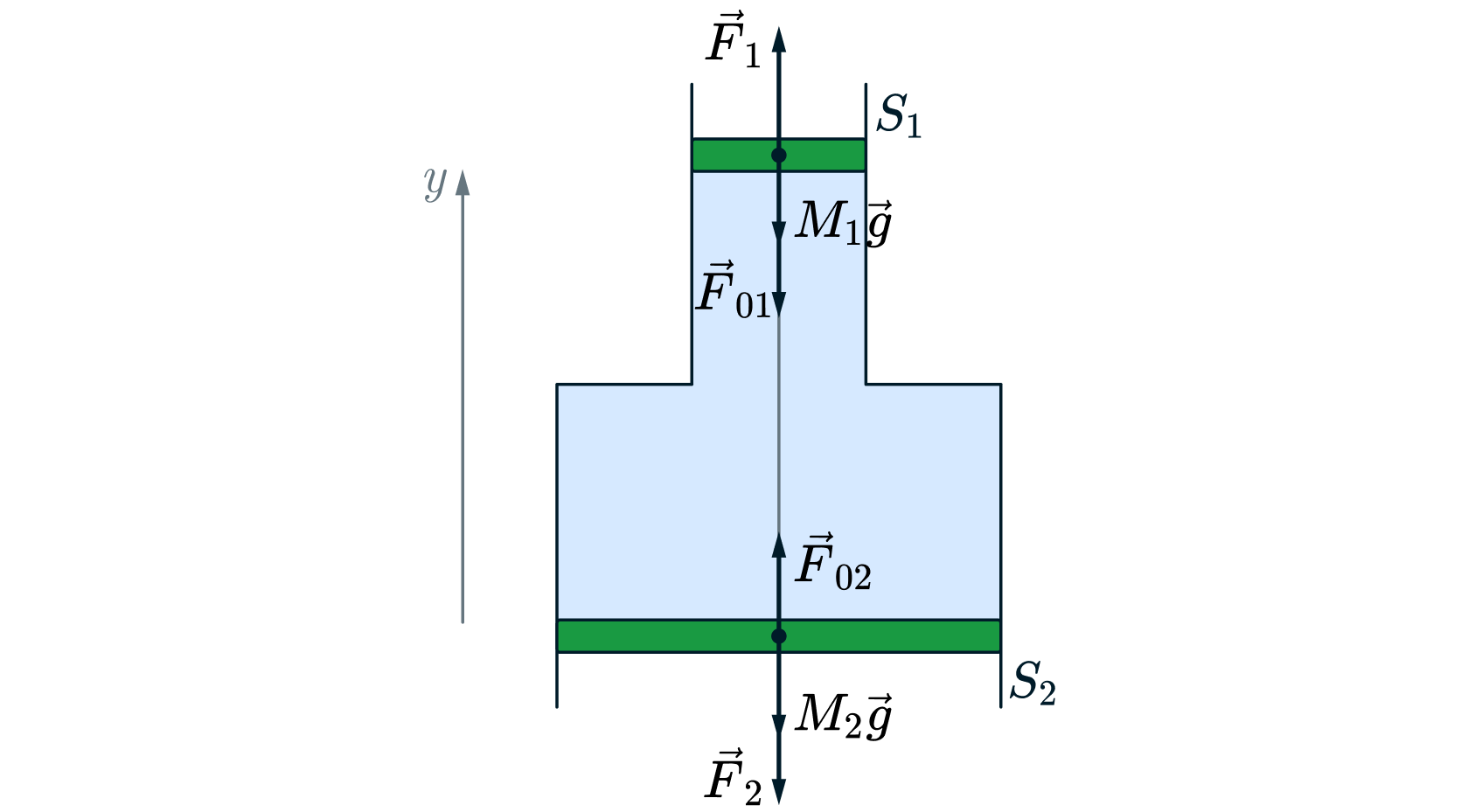
Запишем условия равновесия системы поршни+стержень (внутренние силы реакции стержня по 3 закону Нютона уничтожаются) для начального состояния (до того, как поршни опустились )
где
– начальные силы, с которыми газ внутри действует на поршни
соотвественно,
– силы атмосферного давления, которые действуют на поршни
соотвественно ,
– массы поршней
соотвественно ,
Где в общем случае .
Проецируя на ось (см рисунок) :
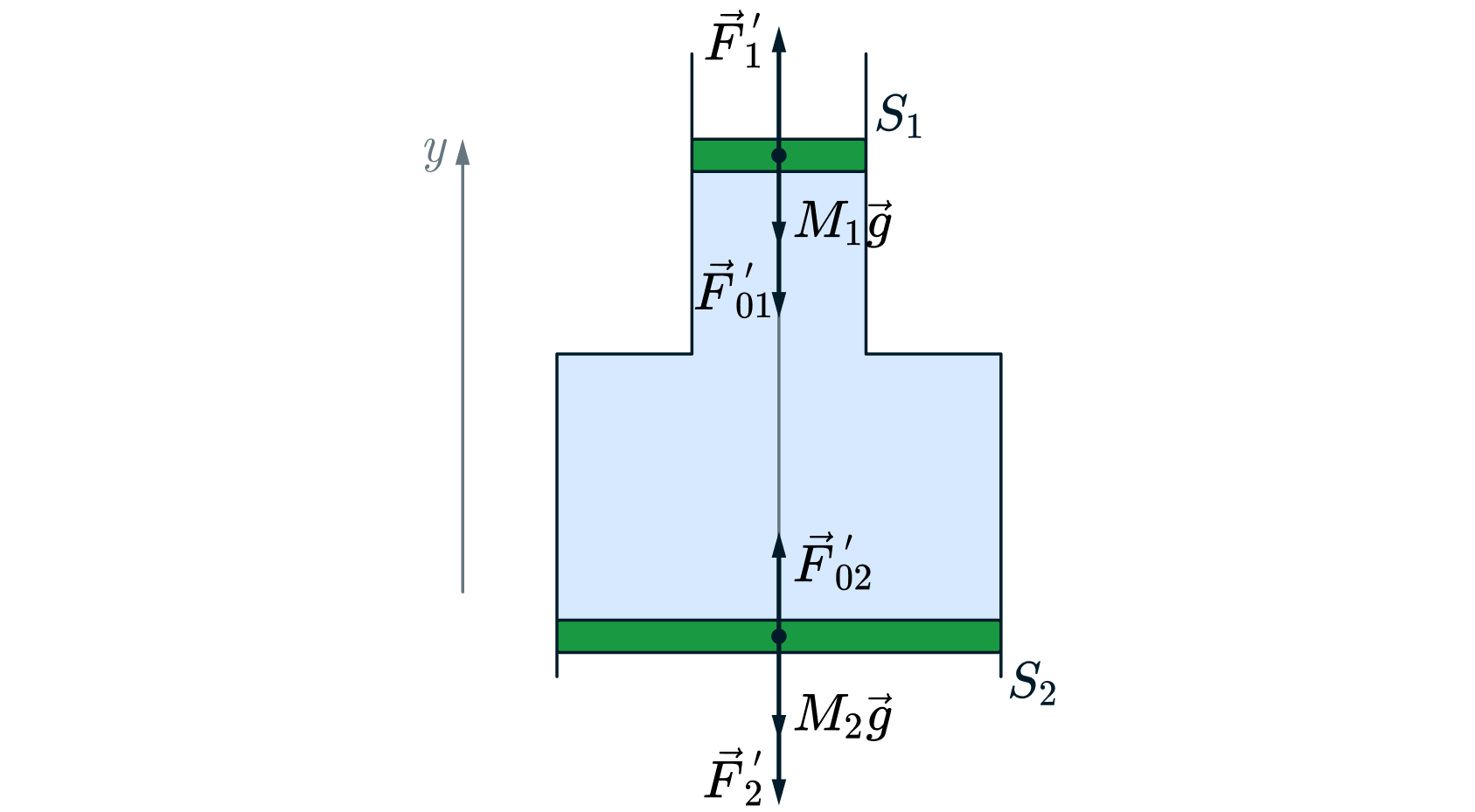
Запишем условия равновесия системы поршни+стержень (внутренние силы реакции стержня по 3 закону Нютона уничтожаются)
для конечного состояния (после того, как поршни опустились на высоту )
где
– силы , с которыми газ внутри действует на поршни
соотвественно после перемещения поршней
вниз.
Проецируя на ось (см рисунок) :
где - давление в сосуде после движения поршней.
Рассматривая разность (1) и (2), получим:
Получаем, что это уравнение имеет решение только если
Тогда в нашем случае имеем изобарный процесс.
Рассмотрим уравнение Менделеева-Клайперона для начального состояния :
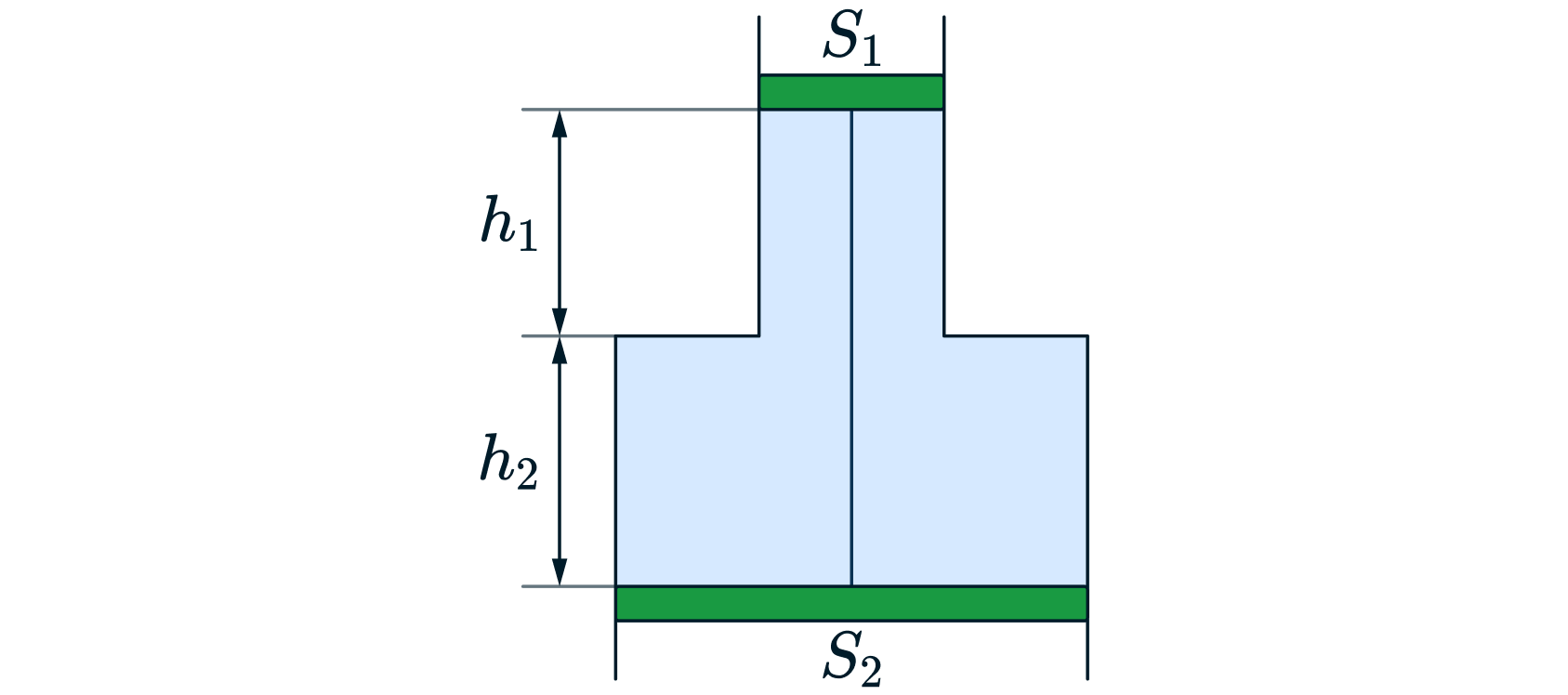
где - начальные высоты у области поршней
соответственно. Рассмотрим уравнение Менделеева-Клайперона для
конечного состояния :
где
(4)-(3):
где .
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




