.02 Термодинамика
Ошибка.
Попробуйте повторить позже
Над одним молем идеального газа совершают цикл (замкнутый процесс), состоящий из двух изохор и двух изобар. Температуры
газов в точках 1 и 3 равны и
соответственно. Определить работу, совершенную газом за цикл, если известно, что точки 2 и 4
лежат на одной изотерме.
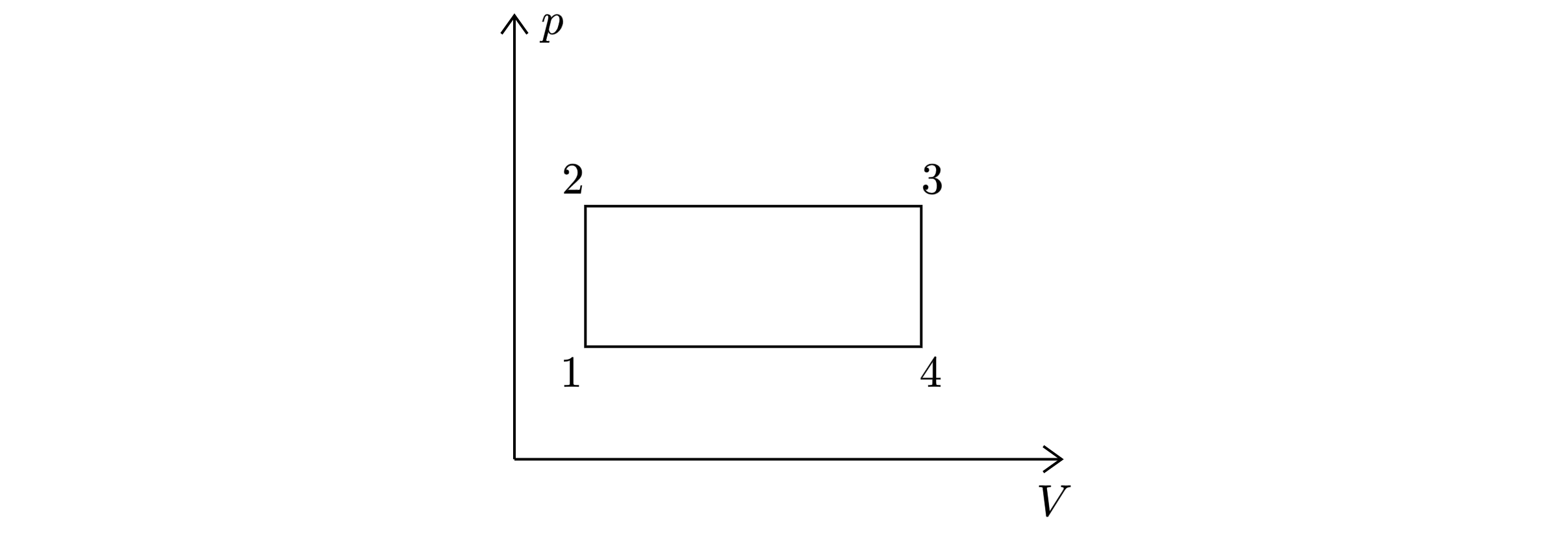
Расширяясь по изобаре (23), газ совершает работу
При сжатии газа по изобаре (4
1)
работа совершается уже над газом, Она равна
Она отрицательна. Полная работа, совершенная
газом, равна
Так как точки 2 и 4 лежат на одной изотерме, то согласно закону Бойля-Мариотта температура газа при этих состояниях
одинакова. Обозначим ее
Тогда
Точки 3 и 4 лежат на одной изохоре, поэтому согласно закону Шарля . Точки 1 и 2 тоже лежат на одной изохоре, поэтому
Приравнивая правые части последних равенств, получаем , откуда
Следовательно
| Критерии оценивания выполнения задачи | Баллы |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае: записана формула работы газа в изобарном процессе. Записана формула нахождения работы газа за весь цикл. Использовано уравнение Менделеева-Клапейрона для нахождения соотношений между величинами (либо законы для изопроцессов)); | |
| II) описаны все вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений, используемых в условии | |
| задачи, и стандартных обозначений величин, используемых при | |
| написании физических законов); | |
| III) представлены необходимые математические преобразования и | |
| расчёты, приводящие к правильному числовому ответу | |
| (допускается решение «по частям» с промежуточными | |
| вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| искомой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| физические законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И (ИЛИ)
| |
| В решении лишние записи, не входящие в решение (возможно, | |
| неверные), не отделены от решения (не зачёркнуты; не заключены | |
| в скобки, рамку и т.п.). | |
|
И (ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и (или) преобразования/вычисления не | |
| доведены до конца. | |
|
И (ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| задачи, без каких-либо преобразований с их использованием, | |
| направленных на решение задачи, и ответа. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения задачи (или утверждение, лежащее в основе решения), | |
| но присутствуют логически верные преобразования с имеющимися | |
| формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения задачи | |
| (или в утверждении, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования с | |
| имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




