18.07 Алгебра. "Гвозди" для квадратичной функции
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра 
при каждом из которых неравенство
имеет решения, и все эти решения принадлежат отрезку ![[−1;2].](/api/latex-service/v1/GetSession/1701/index-cdd92be207b09520bf1553899162bc02.svg)
При 
неравенство принимает вид 
что верно при любом значении 
Так как 
не содержится в отрезке ![[−1;2],](/api/latex-service/v1/GetSession/1700/index-553b9a99233324c8f4085d675236eb0a.svg)
то значение параметра 
не подходит.
Далее будем считать, что 
Тогда старший коэффициент 
следовательно, при каждом фиксированном 
ветви параболы
направлены вверх.
Если дискриминант квадратного трехчлена 
то исходное неравенство не имеет решений. Следовательно, этот случай нам
не подходит.
Если 
то решением неравенства будет отрезок ![[x1;x2],](/api/latex-service/v1/GetSession/1700/index-a08b2dbff28368a87860a836804fae39.svg)
где 
— корни уравнения
Заметим, что при 
решением неравенства будет вырожденный «отрезок» ![[x0;x0],](/api/latex-service/v1/GetSession/1700/index-25bd8f71825fa373c9357a8c8a478b7a.svg)
состоящий из одной точки
— абсциссы вершины параболы.
Изобразим эскиз параболы, удовлетворяющей условию задачи:
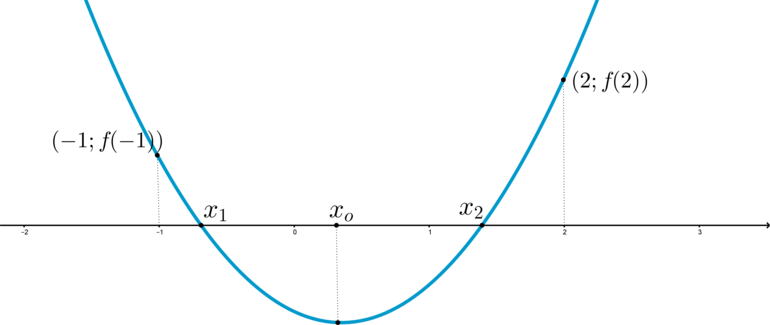
Здесь 
— абсцисса вершины параболы.
Для включения отрезка ![[x1;x2]](/api/latex-service/v1/GetSession/1700/index-15a3b9a8ae39b8012a8fe59deec7d5f6.svg)
в отрезок ![[−1;2]](/api/latex-service/v1/GetSession/1700/index-64b820b6e29bc7d022ed647f861a5900.svg)
необходима система из условий:
![(|f(−1)≥ 0 (|a ∈(−∞; 1− √7]∪ [1+ √7;+ ∞ )
||{f(2)≥ 0 ||{a ≥ 3 √ -
|−1 ≤ x ≤ 2 ⇒ |a ∈(2−∞; −3]∪ [3;+∞ ) ⇒ a∈ [1 + 7;+ ∞ )
||( 02 2 ||( 2
D = 4a ((a− 3) +18)≥ 0 a ⁄=0](/api/latex-service/v1/GetSession/1700/index-bc515476979ada2e0467871ffa1d54ba.svg)
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Ответ может отличаться от верного
невключением граничного значения или
не рассмотрен случай | 3 |
| Для | 2 |
| Рассмотрен верно случай | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
рассмотрена квадратичная
функция, верно наложены все
условия того, чтобы решения неравенства
принадлежали данному отрезку, но в ходе
решения системы допущена ошибка 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
