18.07 Алгебра. "Гвозди" для квадратичной функции
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых один корень уравнения
заключен в промежутке а другой удовлетворяет неравенству
Обозначим
Рассмотрим картинку, которая нам подходит:
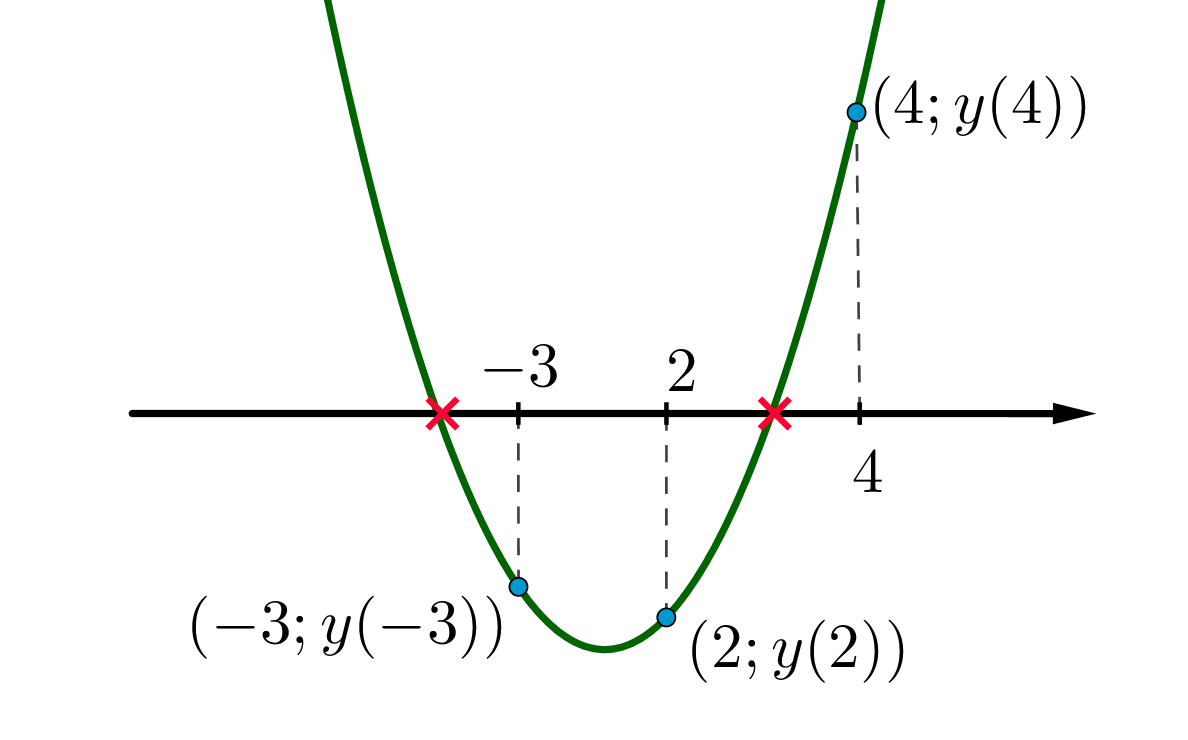
Заметим, что число -3 может находиться во и в
местах. Число 2 может находиться в
или
месте. Число 4
может находиться только в
месте.
Случаи, когда один из корней попадает в или в
место, рассмотрим отдельно. Это значит, что один из корней
уравнения равен -3 или 2. Проверим, при каких
это происходит.
Следовательно, случай нам подходит, а случай
— нет.
Теперь можно считать, что число -3 должно находиться в месте. Число 2 должно находиться в
месте. Число 4
может находиться только в
месте. Это задается следующей системой:
Решая систему и объединяя с предыдущим найденным значением, получаем
_____________________________________________________________________________
Замечание.
Условие на дискриминант здесь необязательно, так как если хотя бы в одной точке для параболы с ветвями вверх
значение функции отрицательно, то автоматически парабола пересекает ось абсцисс в двух точках. Также здесь не
нужно условие на абсциссу вершины, так как число 4 не может попасть в место, иначе оно было бы меньше
-3.
__________________________________________________________________________________________________________________________________________________________________
Расшифровка мест:
— до левого корня
— в левом корне
— между корнями
— в правом корне
— правее правого корня.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Не рассмотрен случай, когда один из
корней может быть равен 2 или | 3 |
| Все неравенства для выполнения условия задания составлены верно, но в решении есть ошибка или оно не завершено | 2 |
| Верное введение функции и её исследование | 1 |
| ИЛИ | |
| верно найдены корни квадратного уравнения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




