.04 Электростатика (Отсутствует в данном номере в ЕГЭ 2026)

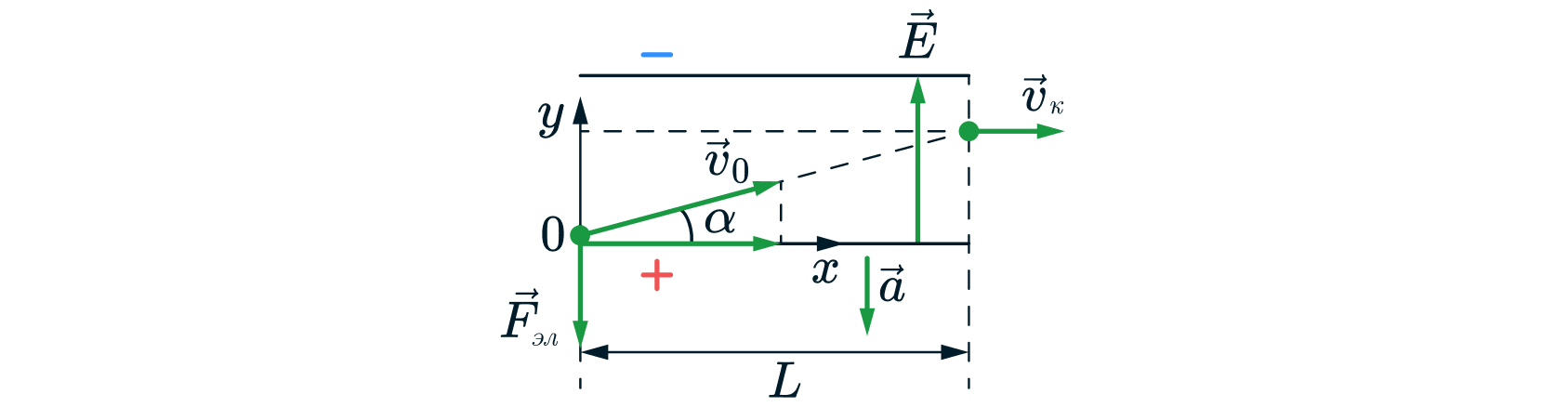
На рисунке схематично показано движение электрона в данной задаче. Здесь – начальная скорость электрона, – угол относительно пластины конденсатора, под котором электрон влетает в конденсатор, – напряжённость электрического поля между пластинами конденсатора, – сила, действующая на электрон со стороны электрического поля конденсатора, – ускорение электрона, – конечная скорость электрона.
1) Начальная энергия электрона равна его кинетической энергии и определяется его начальной скоростью:

–где — масса электрона, — начальная скорость электрона.
Действием сил тяжести на элементарные частицы можно пренебречь.
2) Разложим сложное движение электрона на два простых: вдоль оси параллельной пластинам, и вдоль оси перпендикулярной пластинам.
Начало системы координат поместим в точке влета электрона в конденсатор. Начальные координаты электрона:
и
Начальные скорости электрона:
,
Ускорение следовательно, в направлении движение является равномерным.

3) Из второго закона Ньютона, проекция ускорения на ось :

Следовательно, движение по оси является равноускоренным. Напишем уравнения движения в проекциях на оси и . Закон движения по оси :

(1)

Законы движения по оси :

(2)

(3)

4) Исключим из первого уравнения время и подставим его в третье, получим:

Это уравнение параболы. Мы доказали, что заряженная частица, влетевшая под углом к силовым линиям однородного поля, будет двигаться в этом поле по параболе. В точке вылета , , поэтому

5)Выразим из последнего уравнения время пролета электрона через конденсатор: Из первого уравнения найдем напряженность поля в конденсаторе:

Напряжение на пластинах , т. е. :