.05 Электрические цепи с резисторами (Отсутствует в данном номере в ЕГЭ 2026)
Ошибка.
Попробуйте повторить позже
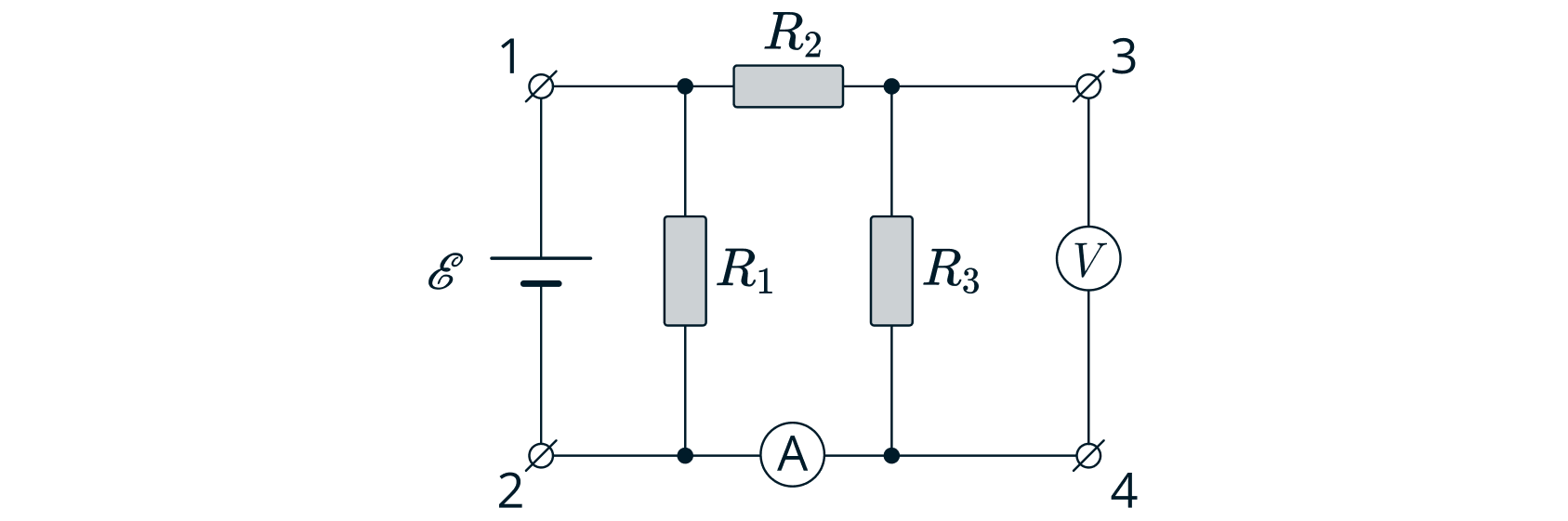
Если между контактами и
схемы, изображённой на рисунке, включить источник напряжения с ЭДС
и малым
внутренним сопротивлением, то идеальный вольтметр, подключённый к контактам
и
, показывает напряжение
, а
идеальный амперметр — силу тока, равную
. Если теперь поменять местами источник и вольтметр, то он показывает
напряжение
. Какой ток показывает теперь амперметр?
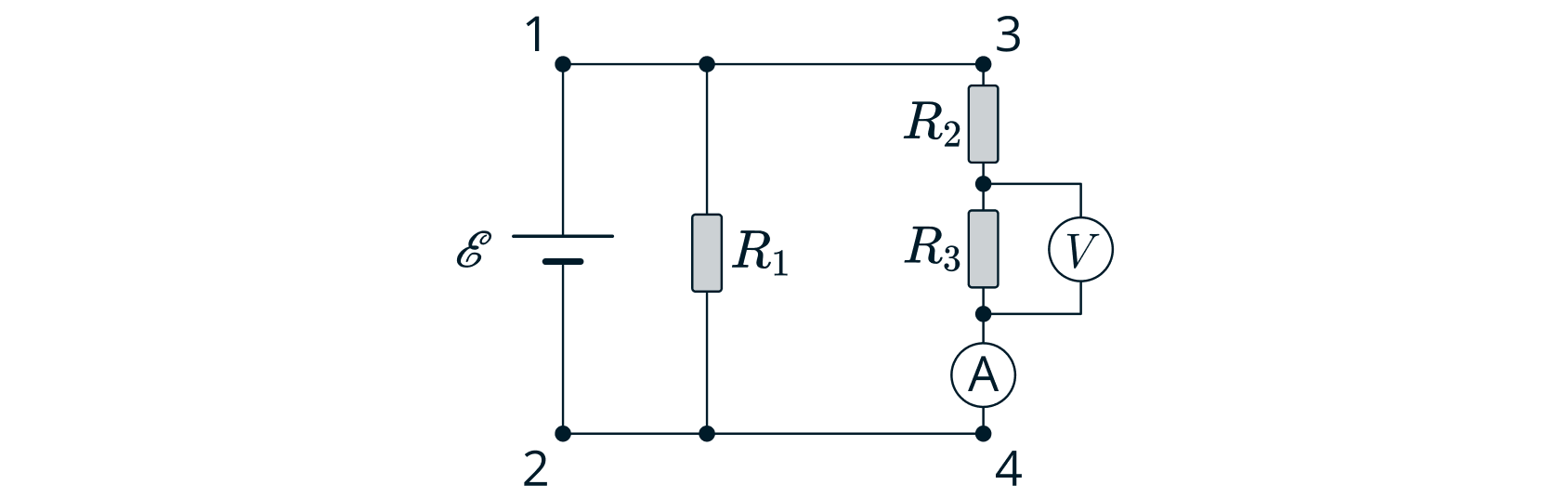
Изобразим эквивалентные схемы подключения для каждого случая.
1)При первом подключении (рис. 1) резисторы и
соединены последовательно, следовательно,
По закону
Ома для участка цепи
, откуда найдем сопротивление третьего резистора:
Поскольку внутренним сопротивлением источника тока можно пренебречь, и резистор соединен параллельно с участком
цепи, содержащим резисторы
и
, то
. Тогда напряжение на втором резисторе
Тогда можем найти
сопротивление второго резистора, используя закон Ома для участка цепи:
2)При втором подключении цепи (рис. 2) резисторы и
соединены последовательно, а резистор
подключен к ним
параллельно. В наших обозначениях показания приборов на второй схеме будем выделять штрихом. Поэтому напряжение на втором
резисторе будет равно
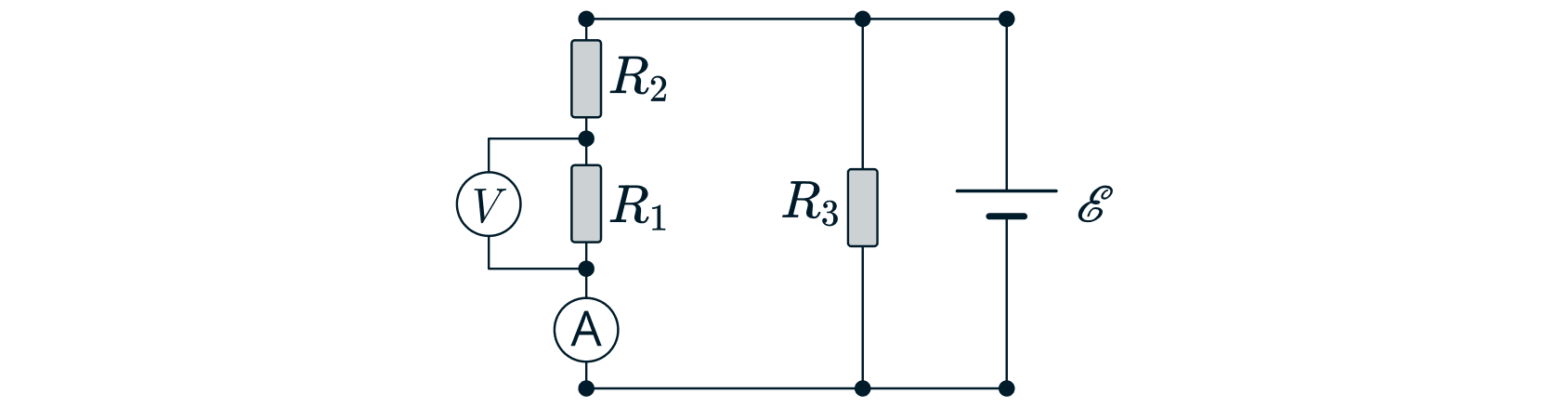
Тогда по закону Ома и учитывая, что при последовательном соединении сила тока равна:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




