.17 Фотоэффект (Отсутствует в данном номере в ЕГЭ 2026)
Ошибка.
Попробуйте повторить позже
Излучение аргонового лазера с длиной волны нм сфокусировано на фотокатоде в пятно диаметром
мм. Работа
выхода фотокатода
эВ. На анод, расположенный на расстоянии
мм от катода, подано ускоряющее напряжение
кВ. Найти диаметр пятна на аноде, на которое попадают фотоэлектроны.
Запишем уравнение Эйнштейна для фотоэффекта:
где – энергия падающего фотона,
– кинетическая энергия фотоэлектрона.
Энергия фотона равна
Кинетическая энергия фотоэлектрона
где – масса электрона,
– его начальная скорость.
Тогда
При этом направление скорости произвольно.

Между анодом и катодом существует однородное электрическое поле, направленное от анода к катоду, напряженность которого равна
В этом поле на электрон действует электрическая сила, направление которой противоположно направлению напряженности поля, так как электрон заряжен отрицательно. Изобразим траекторию движения фотоэлектрона и силы, действующие на него
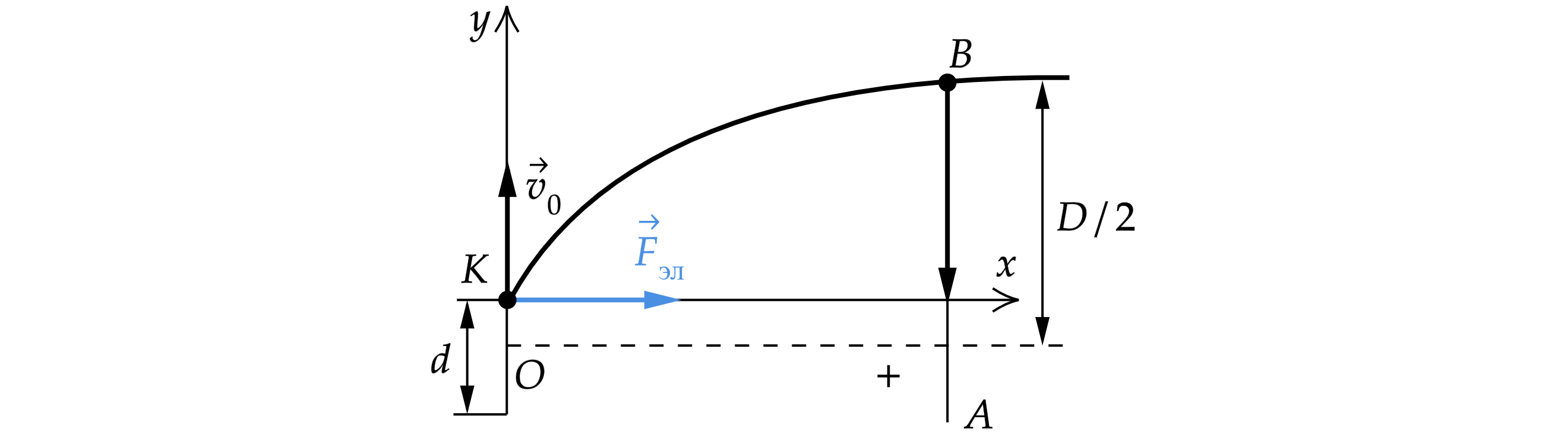
Запишем второй закон Ньютона
где – электрическая сила,
– ускорение фотоэлектрона.
Электрическая сила равна
где – заряд электрона.
Спроецируем второй закон Ньютона на ось
При этом на ось не действует никаких сил, значит, движение вдоль оси
равномерное.
Диаметр пятна на аноде определяется местом вылета фотоэлектрона с поверхности катода и его направлением. Диаметр пятна
будет тем больше, чем ближе к краю вылетит фотоэлектрон и чем больше проекция скорости на ось
, то есть
диаметр будет максимален, когда фотоэлектрон вылетит из края катода и с направлением скорости вдоль оси
(см.
рис. 2). Поместим начало координат в центр катода. Запишем уравнения кинематики для координат на оси
и
.
где – начальная координата фотоэлектрона,
– проекция начальной скорости фотоэлектрона по оси
,
–
время движения.
Тогда
где – начальная координата,
– проекция начальной скорости фотоэлектрона на ось
.
Тогда
Объединим (3) и (4) с учетом (2)
В момент попадания , тогда
Определим координату точки
(в момент
):
При этом это будет радиус пятна, а диаметр равен
Тогда диаметр с учётом (1), (6) и (7) равен
Подставим числа из условия
| Критерии оценивания выполнения задачи | Баллы |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае: уравнение Эйнштейна для фотоэффекта, формула энергии фотонов, формула максимальной кинетической энергии электронов, формула связи напряжения и напряженности, формула силы электрической, второй закон Ньютона, формулы кинематики равномерного и равноускоренного движения); | |
| II) описаны все вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений, используемых в условии | |
| задачи, и стандартных обозначений величин, используемых при | |
| написании физических законов); | |
| III) представлены необходимые математические преобразования и | |
| расчёты, приводящие к правильному числовому ответу | |
| (допускается решение «по частям» с промежуточными | |
| вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| искомой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| физические законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И (ИЛИ)
| |
| В решении лишние записи, не входящие в решение (возможно, | |
| неверные), не отделены от решения (не зачёркнуты; не заключены | |
| в скобки, рамку и т.п.). | |
|
И (ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и (или) преобразования/вычисления не | |
| доведены до конца. | |
|
И (ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| задачи, без каких-либо преобразований с их использованием, | |
| направленных на решение задачи, и ответа. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения задачи (или утверждение, лежащее в основе решения), | |
| но присутствуют логически верные преобразования с имеющимися | |
| формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения задачи | |
| (или в утверждении, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования с | |
| имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




