.03 Динамика

Обоснование

1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.

2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.

3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.

4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень горизонтальной поверхности.

5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.

Решение

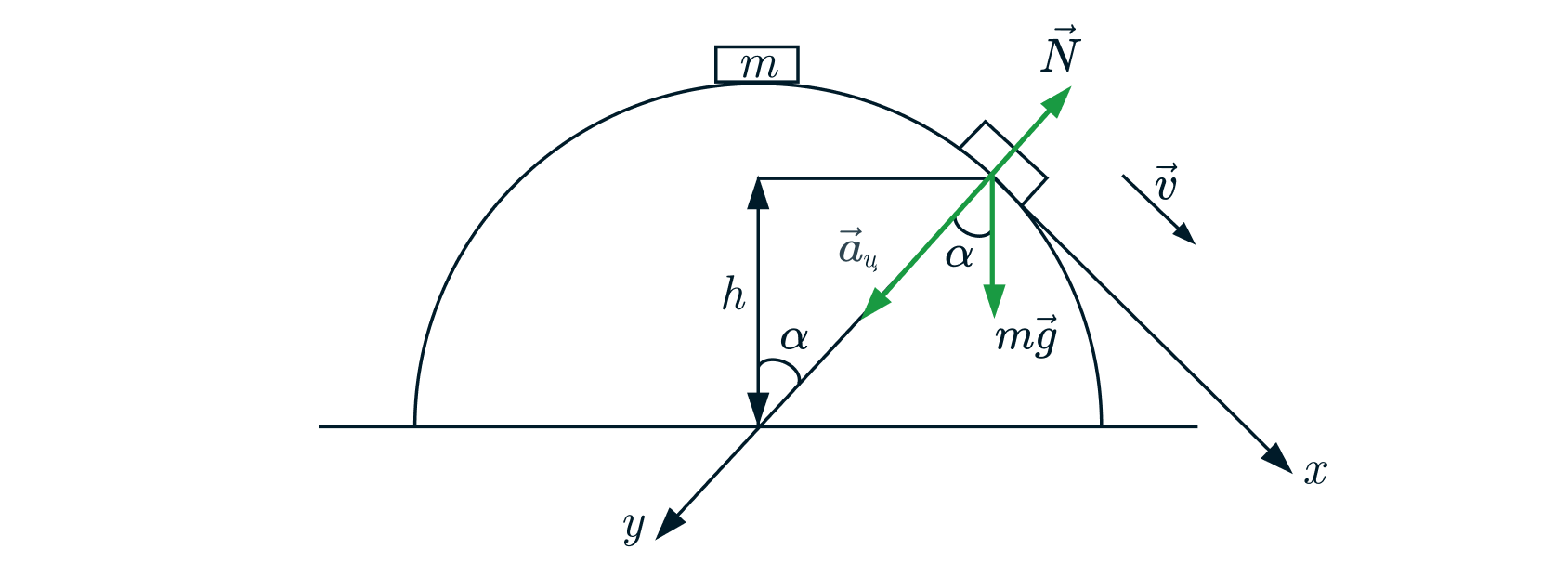
Во время скольжения тела по полусфере на него действуют сила тяжести и сила реакции направленная вдоль продолжения радиуса.Т.к. тело движется по окружности, то оно обладает центростремительным ускорением направленное к центру полусферы, – скорость в какой-либо точке полусферы. Выберем удобные нам оси и Сделаем рисунок с указанием сил, действующих на тело:

Спроектируем силы на ось по второму закону Ньютона получаем:

(1)

Так как скорость тела возрастает, то в некоторой точке обратится в ноль, т.е. тело оторвется от поверхности полусферы.

Пусть высота, на которой происходит отрыв, равна Полная механическая энергия тела в верхней точке движения . Полная механическая энергия в точке отрыва: Так как трения нет, то полная механическая энергия тела сохраняется:

(2)

Из рисунка найдём косинус угла :

(3)

Подставим значения и из уравнений (2) и (3) в уравнение (1), получим:

В момент отрыва скорость тела:

C помощью тригонометрических формул найдём синус угла :

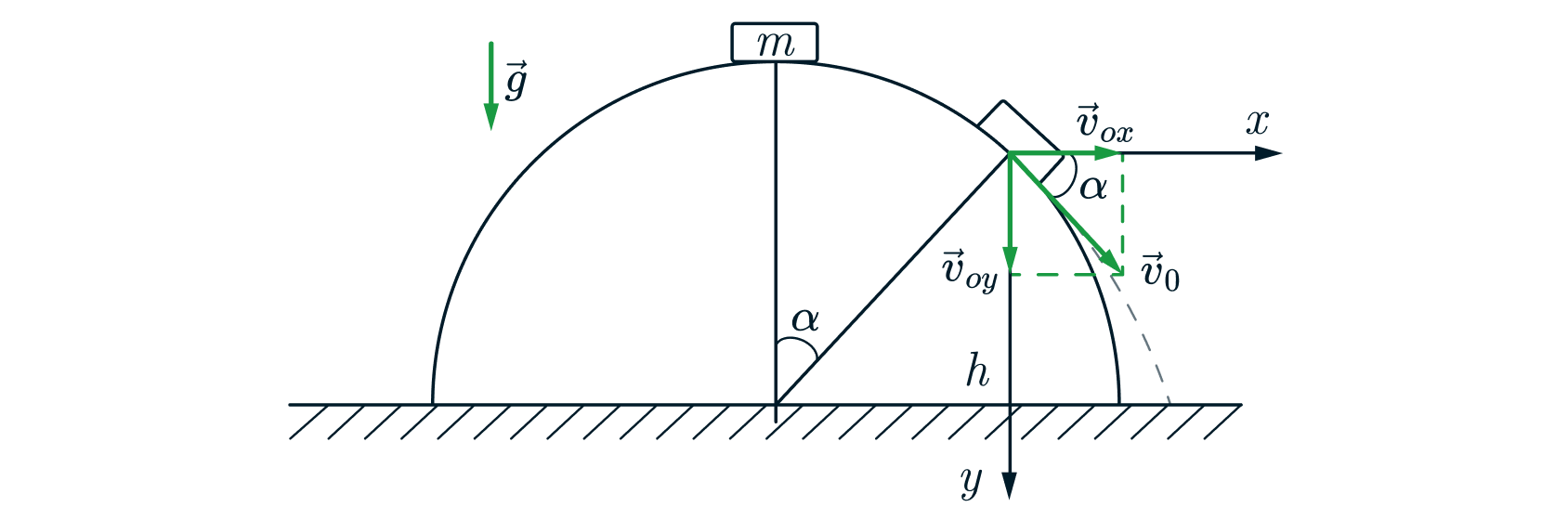
Теперь рассмотрим задачу с точки зрения кинематики. Сделаем рисунок с указанием начальных скоростей тела:

После отрыва от полусферы движение происходит только под действием силы тяжести, причем скорость тела сначала направлена под углом к горизонту. Значит, тело движется по параболе.

Начальные координаты тела: Начальные скорости: Закон движения по оси :

В момент падения , где - искомое время. Получаем квадратное уравнение:

корни которого:

Берем положительный корень: