.03 Динамика
Ошибка.
Попробуйте повторить позже
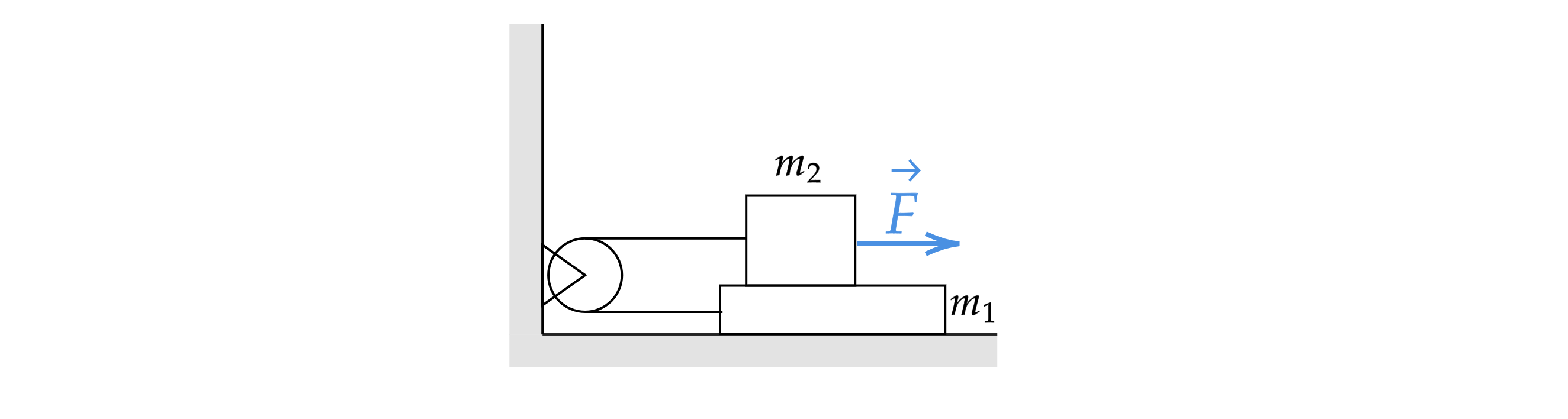
На горизонтальном столе доска массой на которую поместили брусок массой
Брусок и доска соединены
через идеальный блок (лёгкий, гладкий) лёгкой и нерастяжимой нитью. Брусок тянут с силой
Коэффициент трения
между доской и бруском равен
, а поверхность стола гладкая. Определите длину доски, если спустя время
брусок
соскальзывает с доски. Изначально брусок находился на краю доски. Обоснуйте применимость законов, используемых для решения
задачи.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Поскольку тела связаны нерастяжимой нитью их ускорения равны.
3. Поскольку тела связаны легкой нитью, блок идеальный и трение отсутствует, модули сил натяжения нитей, действующих на тела равны.
4. Поступательное движение тел в ИСО будем описывать при помощи законов Ньютона.
Рассмотрим задачу с точки зрения динамики:
Бруски движутся под действием сил, которые изображены на рисунке
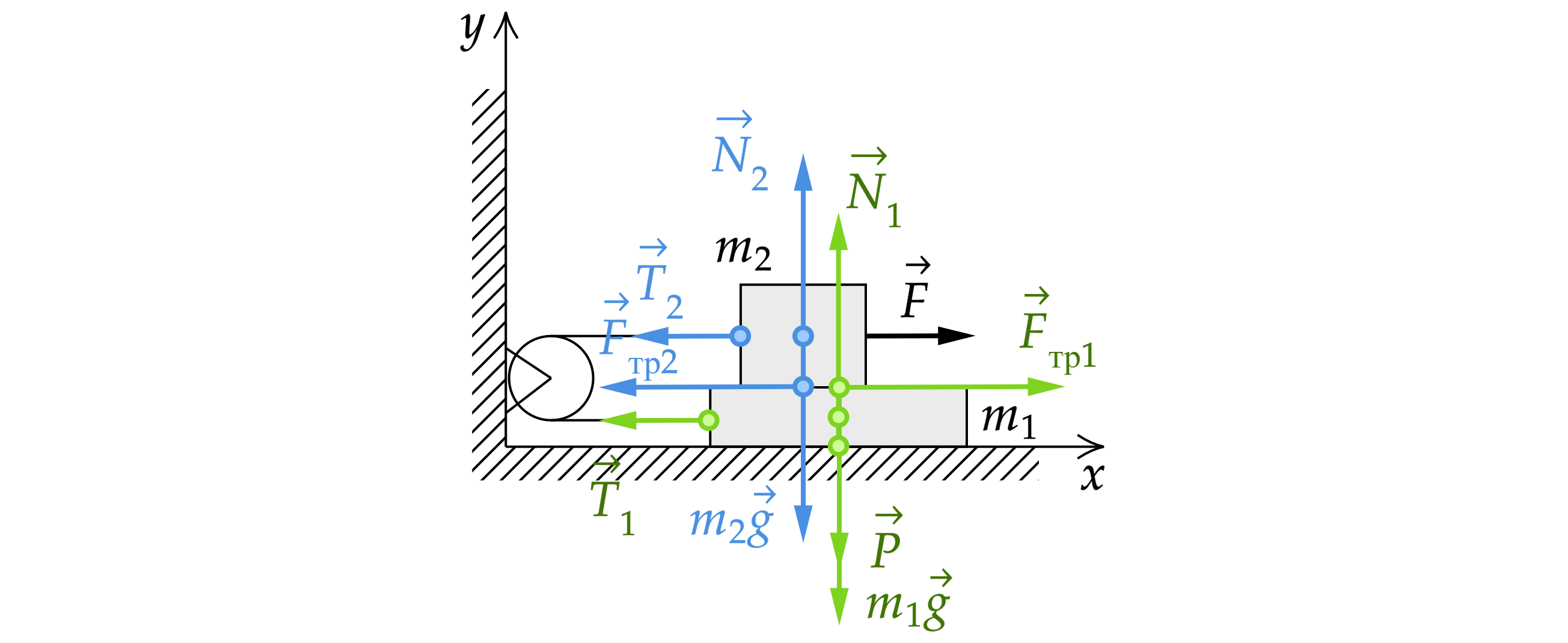
где и
– модули силы натяжения нити,
и
– модули силы трения,
и
– сила тяжести,
– сила
реакции опоры стола,
– сила реакции доски,
– вес бруска.
Запишем второй закон Ньютона для бруска и доски
Так как нить нерастяжимая, то . По третьему закону Ньютона
,
и
.
Спроецируем (1) на оси
и
|
|
Аналогично для (2)
|
|
Сила трения же равна
Тогда
|
|
Сложим два уравнения
Теперь применим кинематический подход:
Брусок двигается относительно доски равноускоренно и прямолинейно, тогда его движение описывается законом:
где – момент времени,
– координата бруска в момент времени
,
– скорость бруска в начальный момент времени,
–
ускорение бруска относительно доски (
).
В момент времени уравнение приобретёт вид:
Подставим формулу для ускорения в формулу для силы:
|
|
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




