.03 Динамика

Обоснование 1. Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью стола.
2. Тела движутся поступательно, поэтому будем их описывать моделью материальной точки. Следовательно, можно использовать второй закон Ньютона, сформулированный для материальных точек. Силы, действующие на тела, постоянны, поэтому движение бруска и доски равноускоренно.
3. Так как нить нерастяжима, ускорения бруска и доски относительно стола равны по модулю и противоположны по направлению:

4. Так как блок и нити невесомы и трением в оси блока можно пренебречь, то силы натяжения нити, действующие на доску и брусок, одинаковы:

5. Силы трения, действующие на брусок и доску, равны друг другу и противоположны по направлению по третьему закону Ньютона:

6. Модули сил нормальной реакции доски и давления бруска на доску также равны друг другу по третьему закону Ньютона:

Решение
1) Укажем силы, действующие на брусок (красным) и на доску (синим).

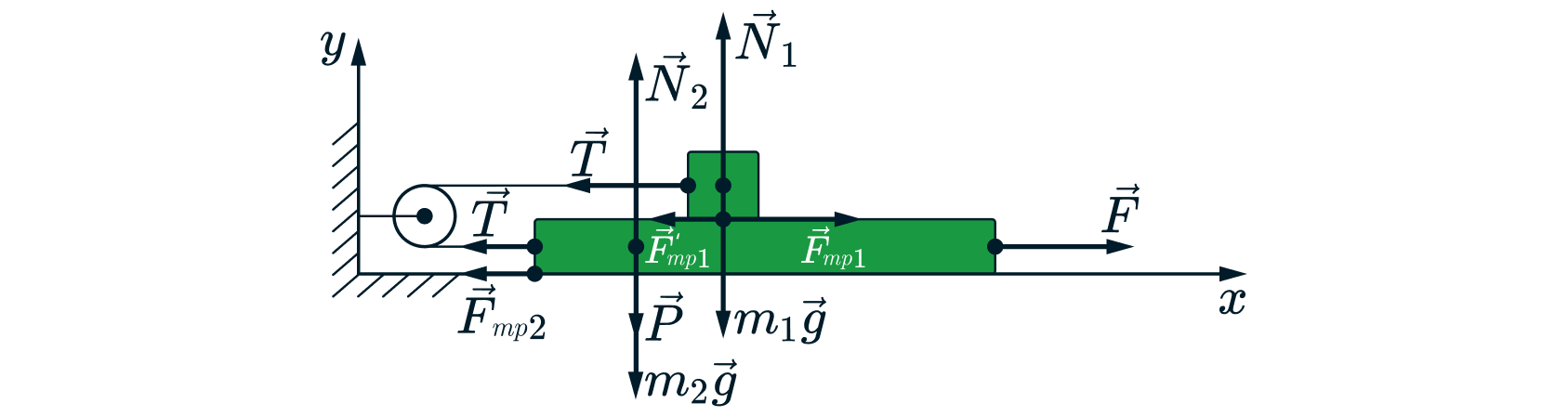
Здесь – сила натяжения нити, – сила реакции опоры доски, – сила реакции опоры стола, – сила трения между доской и бруском, – сила трения между столом и доской.
Ускорения доски и бруска равны, так как они связаны нерастяжимой нитью.
Запишем второй закон Ньютона для доски и бруска

Здесь – ускорение, по 3 закону Ньютона.
Сила трения равна:

Спроецируем второй закон Ньютона на вертикальную ось:

Спроецируем второй закон Ньютона на горизонтальную ось, с учётом (1):

Сложим два уравнения:

Отсюда выразим :