.03 Динамика
Ошибка.
Попробуйте повторить позже
Человек массой , упираясь ногами в ящик массой
, подтягивает его с помощью каната, перекинутого через блок, по
наклонной плоскости с углом наклона
(см. рисунок). С какой минимальной силой надо тянуть канат человеку, чтобы
подтянуть ящик к блоку? Коэффициент трения скольжения между ящиком и наклонной плоскостью равен
.
Части каната, не соприкасающиеся с блоком, параллельны наклонной плоскости. Массами блока и каната пренебречь
(МФТИ, 1998)

Расставим силы, действующие на ящик (красным) и человека (синим).
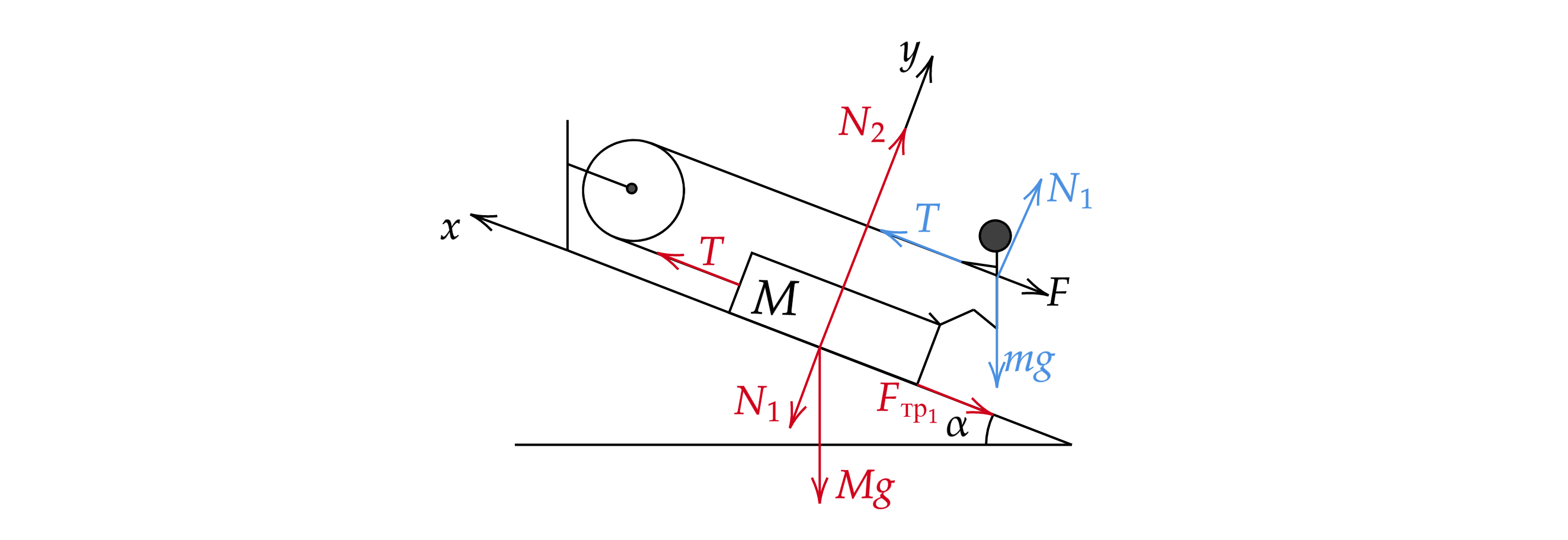
По третьему закону Ньютона . Данную систему можно заменить на аналогичную массой
.
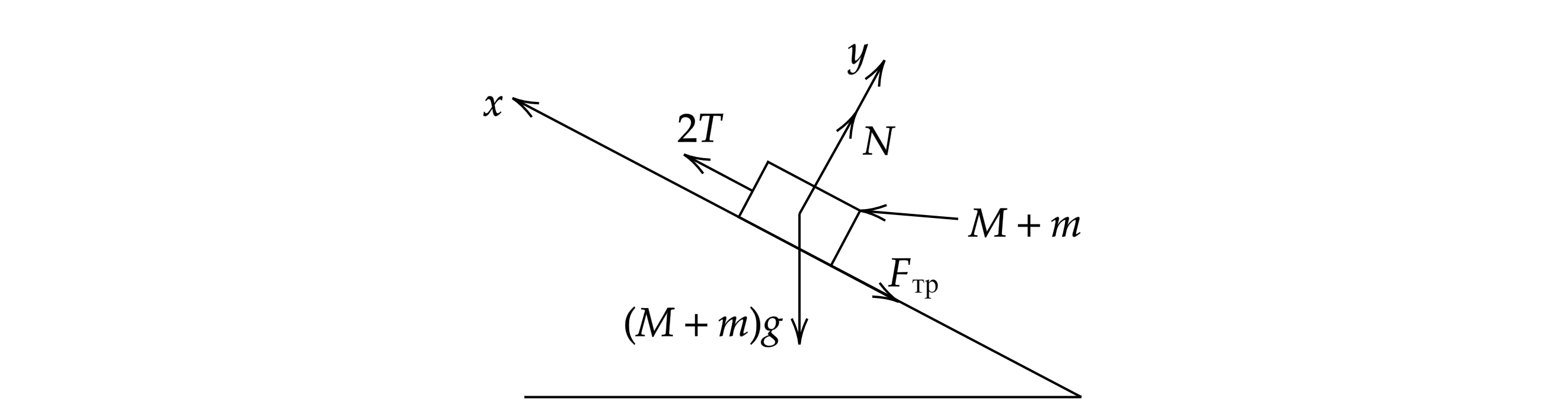
где – сила реакции опоры,
– сила трения,
– сила натяжения нити.
Запишем второй закон Ньютона:
где – ускорение составного тела.
Спроецируем второй закон Ньютона на оси и
:
|
|
Сила трения равна:
Тогда
При этом сила минимальна, если
. Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




