.03 Динамика
Ошибка.
Попробуйте повторить позже
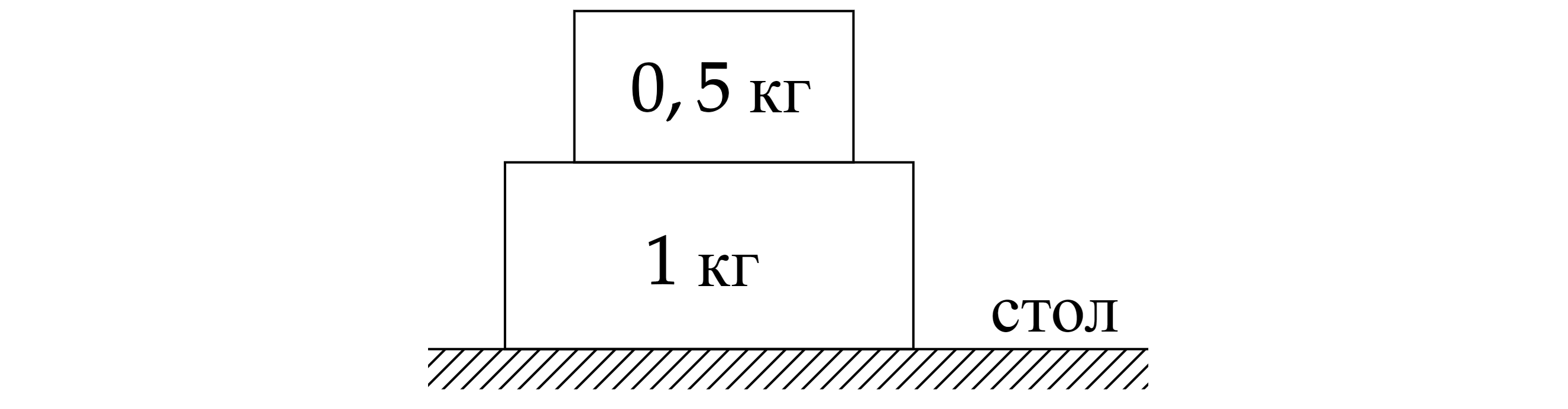
Деревянный брусок массой 0,5 кг лежит на деревянном бруске массой 1 кг. Коэффициент трения между брусками равен 0,35, а коэффициент трения между нижним бруском и столом равен 0,2. Какую максимальную силу можно приложить к большему бруску, чтобы меньший брусок оставался в покое относительно него? Обоснуйте применимость законов, используемых для решения задачи.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Так как тела движутся поступательно, то для них можно использовать модель материальной точки.
3. Движение материальной точки в ИСО будем описывать используя законы Ньютона.
Решение
Для того, чтобы брусок оставался в покое относительно большего, необходимо, чтобы бруски двигались с одним ускорением. Рисунок для меньшего бруска:
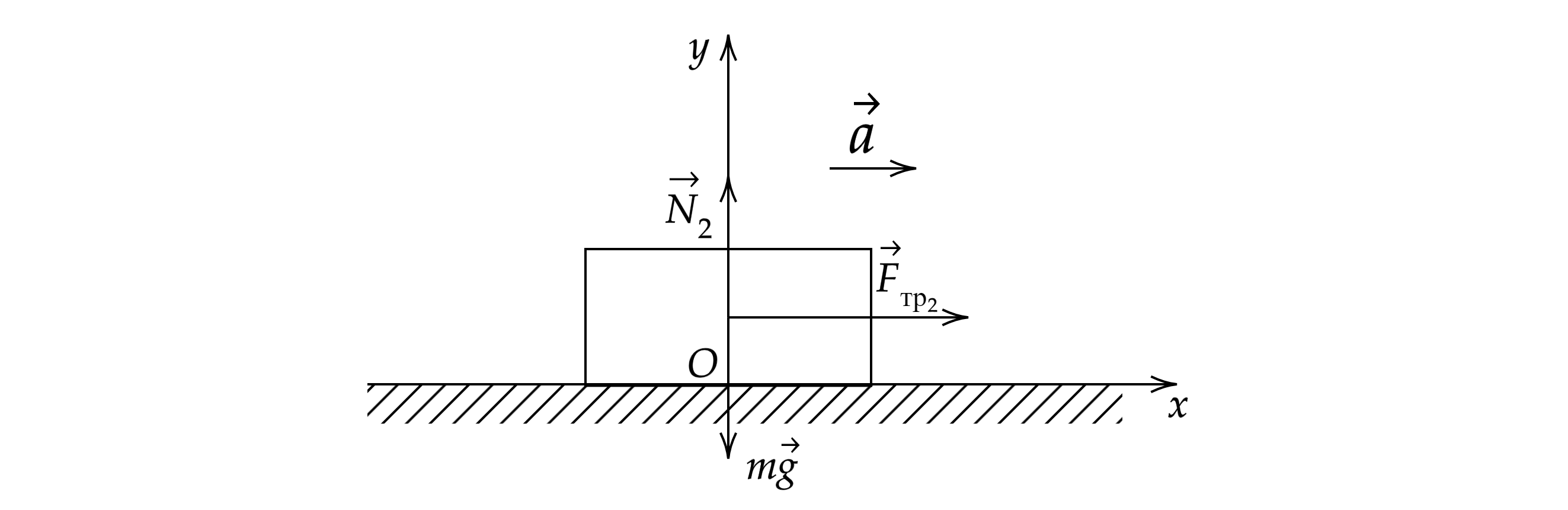
Запишем второй закон Ньютона в проекциях на оси и
|
|
Учитывая, что , получим:
,
,
По 3 закону Ньютона найдем вес верхнего тела: Следовательно, на нижнее тело будет дополнительно давить сила
равная
Рисунок и второй закон Ньютона для большего бруска:
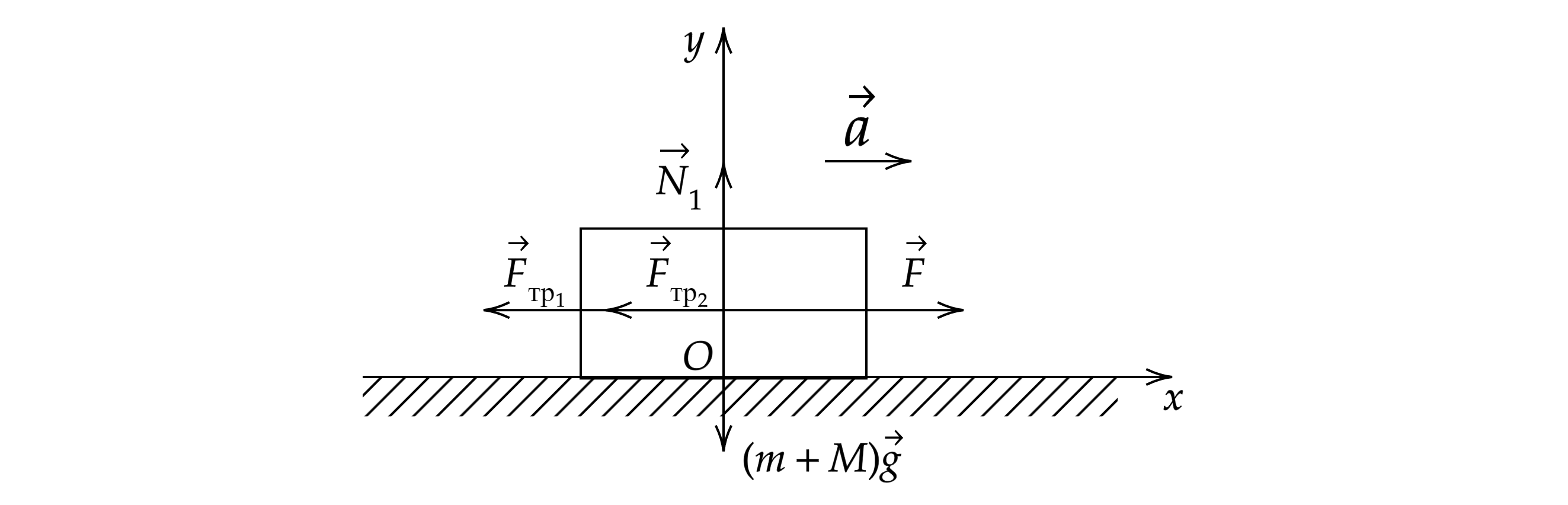
|
|
Учитывая, что , получим:
Откуда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




