.03 Динамика
Ошибка.
Попробуйте повторить позже
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами и
связанные нерастяжимой невесомой нитью длиной
Нить закрепили на оси так, что грузы располагаются по разные
стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). При вращении штанги с
частотой 900 об/мин модуль силы натяжения нити, соединяющей грузы,
Определите длину нити
Какие законы Вы
используете для решения задачи? Обоснуйте их применение.

Источники:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Размеры грузов малы по сравнению с размерами штанги, поэтому будем описывать грузы моделью материальной точки.
3. При вращении тела будут двигаться по окружности, из пункта 1 описывать их движение будем вторым законом Ньютона, при этом ускорение тел будет центростремительное.
4. Так как по условию нить легкая, то силы натяжения нити будут одининаковы для обоих грузов.
5. Так как грузы находятся на одном стержне, то полный оборот они совершают за одно и то же время, т.е. периоды их
обращения равны. Период можно рассчитать по формуле , так как периоды равны, то равны и угловые скорости
вращения. Период и частота связаны соотношением
, а так как периоды равны то и частоты тоже будут
равны.
Решение
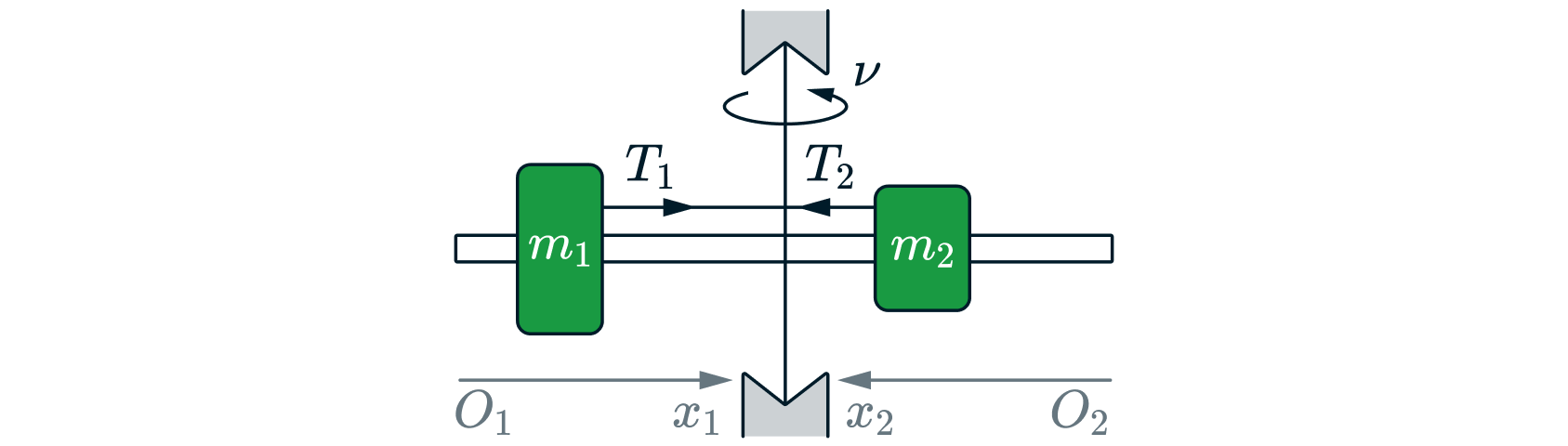
Для каждого груза выберем инерциальную систему отсчёта, ось которой направлена вдоль штанги к оси вращения (см. рисунок), и запишем в проекциях второй закон Ньютона для грузов:
|
|
где ,
– центростремительные ускорения грузов,
– циклическая частота,
– радиус
обращения.
Так как , а
, то найдем радиус обращения первого груза из системы уравнений и силу натяжения
нити.
Отсюда длина нити
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




