.04 Законы сохранения в механике
Ошибка.
Попробуйте повторить позже
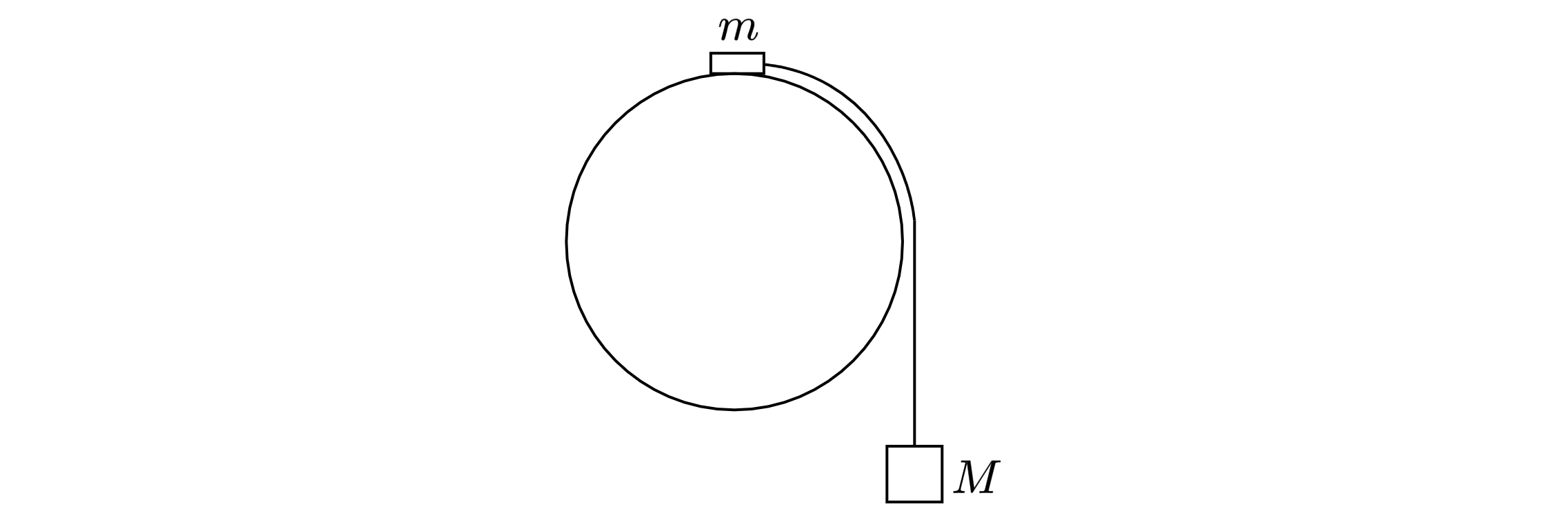
Система из грузов и
связывающей их лёгкой нерастяжимой нити в начальный момент покоится вертикальной плоскости,
проходящей перпендикулярно оси О закреплённой сферы. Груз
находится в точке
на вершине сферы (см. рисунок). В ходе
возникшего движения груз отрывается от поверхности сферы, пройдя по ней дугу
. Найдите массу
, если
кг.
Размеры груза
ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический
рисунок с указанием сил, действующих на грузы. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Основная волна 2012
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать тела моделью материальной точки.
3. Используя пункты 1 и 2 описывать момент отрыва будем использовать второй закон Ньютона относительно ИСО.
4. Так как нить легкая и трение отсутствует, натяжение нити в любой ее точке одинаково. Так как нить нерастяжимая то тела будут двигаться с одинаковыми скоростями.
5. В процессе движения на грузы действуют непотенциальные силы - сила реакции опоры и силы натяжения
нити. Сила реакции опоры перпендикулярна скорости, поэтому её работа равняется нулю. Силы натяжения нити
действующая на груз сонаправлена с ее скоростью, сила натяжения нити действующая на груз
направлена
против ее скорости. Значит, суммарная работа двух этих сил равняется нулю, следовательно выполняется закон
сохранения энергии для системы тел. (Нить - является идеальной связью, суммарная работ ее в системе равняется
нулю).
6. Так как груз будет двигаться по окружности, то он будет обладать центростремительнм ускорением, направленным к
центру окружности вращения.
7. За нулевой уровень потенциальной энергии примем уровень центра сферы.
Решение
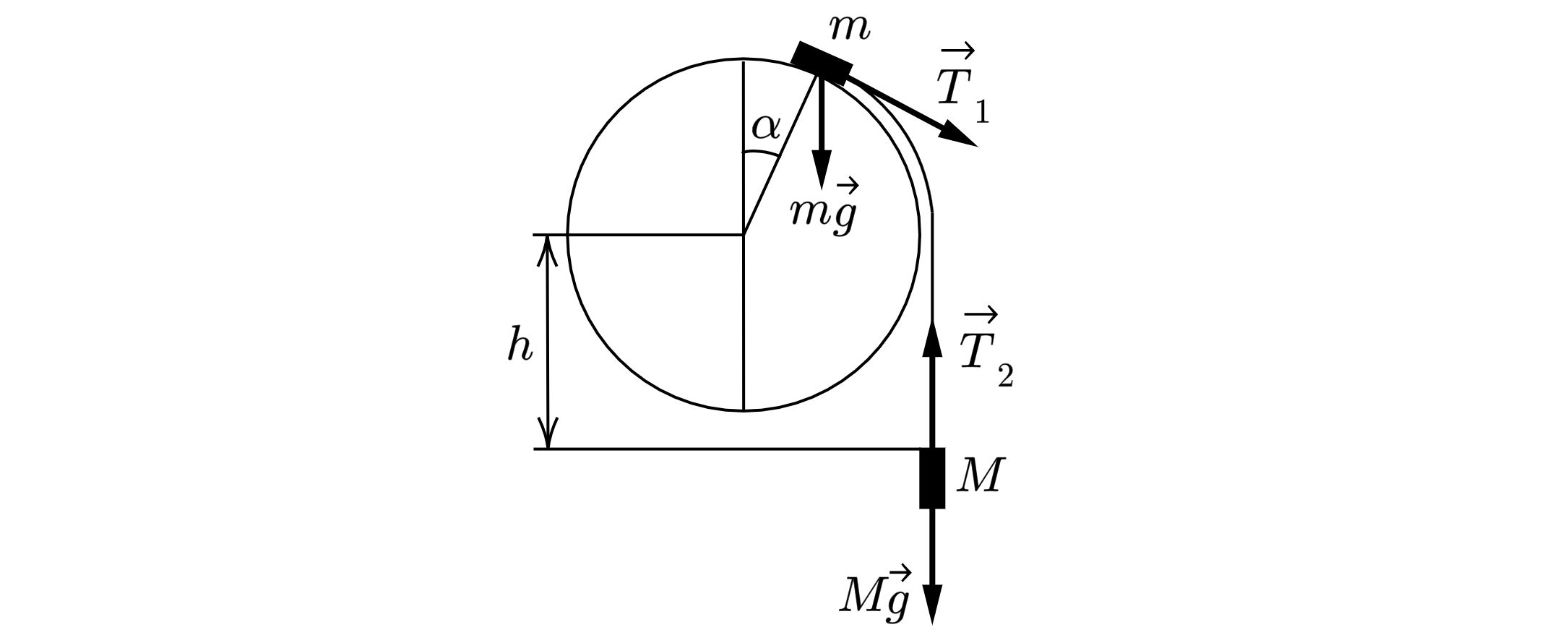
Найдем модуль скорости груза в точке отрыва его от поверхности сферы. Для этого приравняем друг другу значения
механической энергии системы грузов в начальном состоянии и в состоянии, когда груз m находится в точке отрыва (потенциальную
энергию грузов в поле тяжести отсчитываем от уровня центра сферы, в начальном состоянии груз
находится ниже центра
сферы на величину
):
где – радиус трубы,
. Отсюда
Груз в точке отрыва еще движется по окружности радиусом
, но уже не давит на сферу. Поэтому его
центростремительное ускорение вызвано только силой тяжести, так как сила
направлена по касательной к сфере (см.
рисунок):
Подставляя сюда значение , получим:
Отсюда:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обосновано применение второго закона Ньютона для, сказано, что в момент отрыва сила реакции опоры обращается в ноль
4. Обосновано применение закона сохранения энергии
5. Обосновано равенство скоростей грузов
6. Введен нулевой уровень потенциальной энергии
7. Обосновано равенство натяжения нитей
8. Обосновано наличие центростремительного ускорения
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности; применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения механической энергии,
формула для величины центростремительного ускорения);
II) описаны все вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, и обозначений, используемых в условии задачи);
III) представлен схематический рисунок с указанием сил, поясняющий решение;
IV) проведены необходимые математические преобразования (допускается вербальное указание на их
проведение) и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям»
с промежуточными вычислениями);
V) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны необходимые положения теории и физические законы, закономерности; проведены
необходимые преобразования, и представлен правильный ответ с указанием единиц измерения искомой
величины. Но имеется один из следующих недостатков. Записи, соответствующие одному
или нескольким пунктам: II, III, IV, – представлены не в полном объёме или отсутствуют
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
ИЛИ
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
ИЛИ
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца.
ИЛИ
При ПОЛНОМ решении отсутствует пункт V, или в нём допущена ошибка 1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на
решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




