.04 Законы сохранения в механике

Сделаем рисунок сил

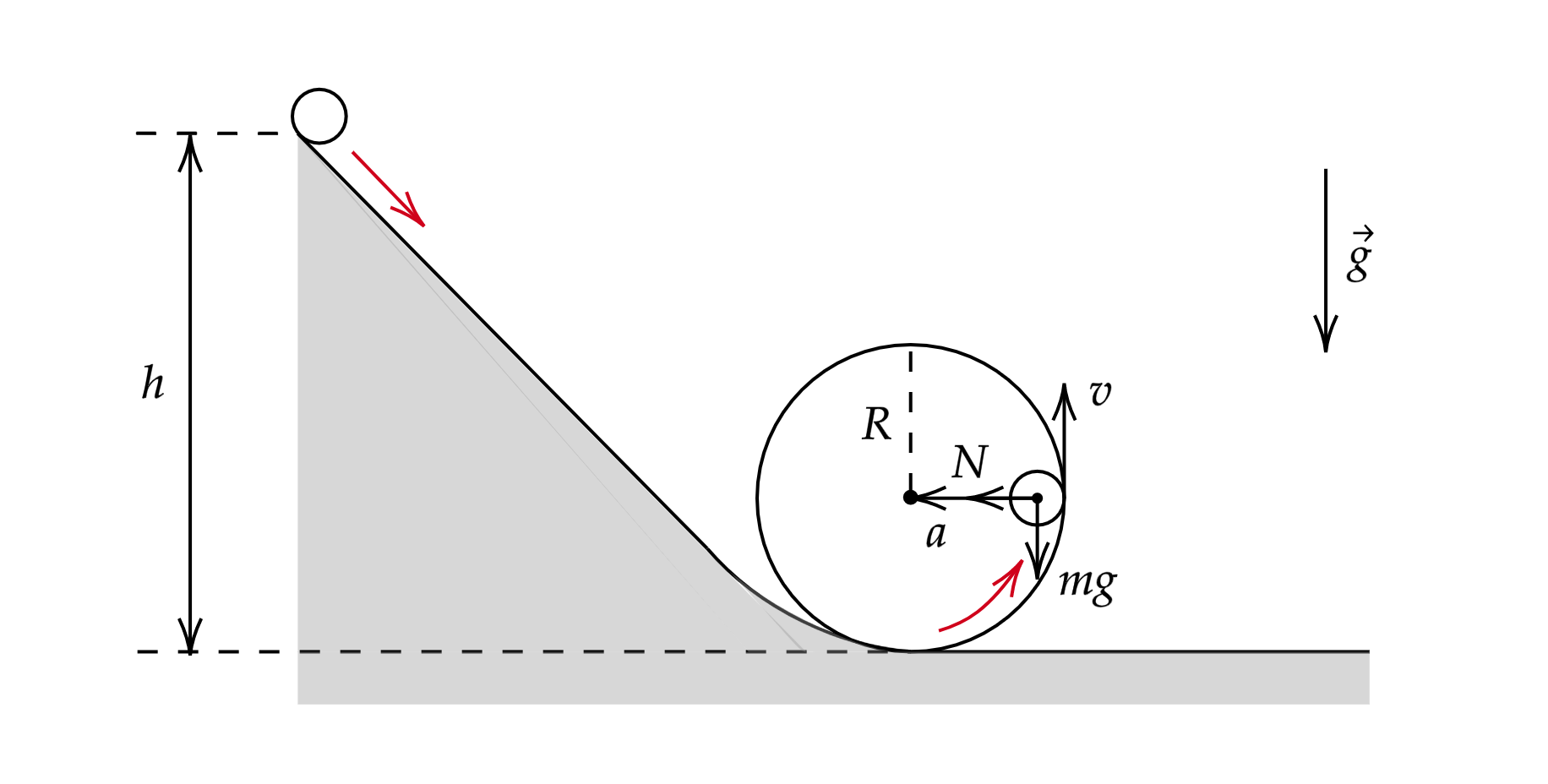
Где – сила реакции опоры, – полное ускорение, – сила тяжести, – скорость шарика.
а) Скорость тела направлена по касательной к окружности, значит, тело должно находиться в крайней правой (левой) точке петли (см. рис.). Найдем скорость шарика из закона сохранения энергии

Запишем второй закон Ньютона:

Запишем второй закон Ньютона на вертикальную ось

По горизонтальной оси у тела присутствует центростремительное ускорение, равное

Откуда полное ускорение

б) Пусть угол между центростремительным ускорением и силой тяжести равен , тогда скорость на искомой высоте равна

Рассмотрим два случая. Первый случай, сила тяжести сонаправлена с силой реакции опоры

По условию , тогда

Откуда высота

Теперь рассмотрим случай разнонаправленности и

Косинус не может быть больше 1, следовательно, такая ситуация невозможна