.04 Законы сохранения в механике
Ошибка.
Попробуйте повторить позже
Маленький шарик массой подвешен на лёгкой нерастяжимой нити длиной
которая разрывается
при некоторой силе натяжения
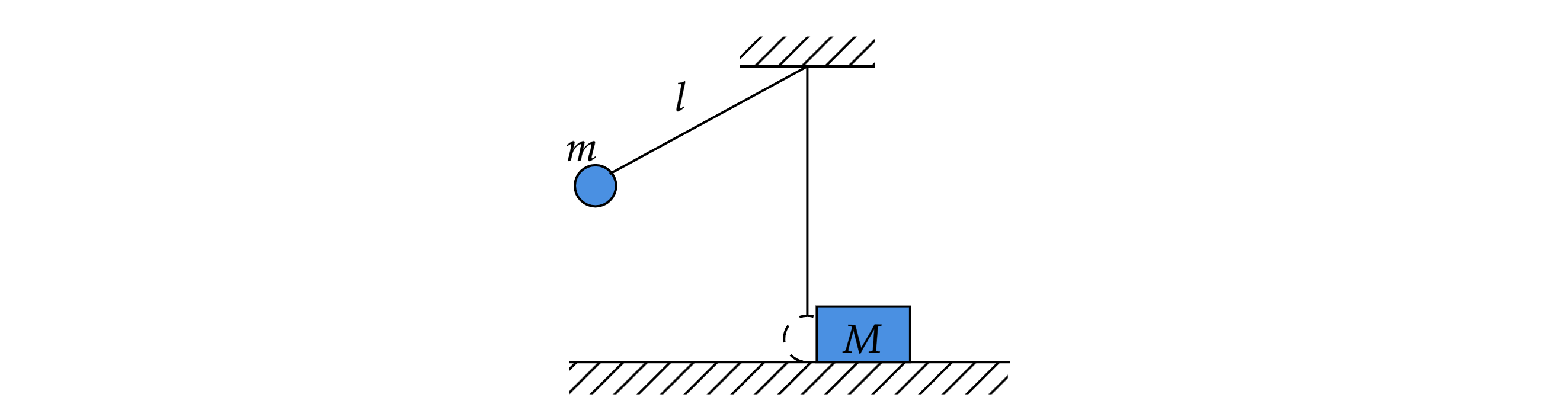
Шарик отведён от положения равновесия (оно показано на рисунке пунктиром) и
отпущен. Когда шарик проходит положение равновесия, нить обрывается, и шарик тут же абсолютно неупруго
сталкивается с бруском массой
лежащим неподвижно на гладкой горизонтальной поверхности стола.
Скорость бруска после удара
Определите величину силы
Считать, что брусок после удара движется
поступательно.
Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать тела моделью материальной точки.
3. Будем считать, что время соударения мало, и действие внешних сил во много раз меньше сил внутренних, поэтому момент соударения будем описывать с использованием закона сохранения импульса.
4. Поскольку шар является материальной точкой, его движение в ИСО будем описывать при помощи второго закона Ньютона.
5. Поскольку шар движется по дуге окружности радиуса , он будет обладать центростремительным ускорением, направленым
к центру окружности.
Решение
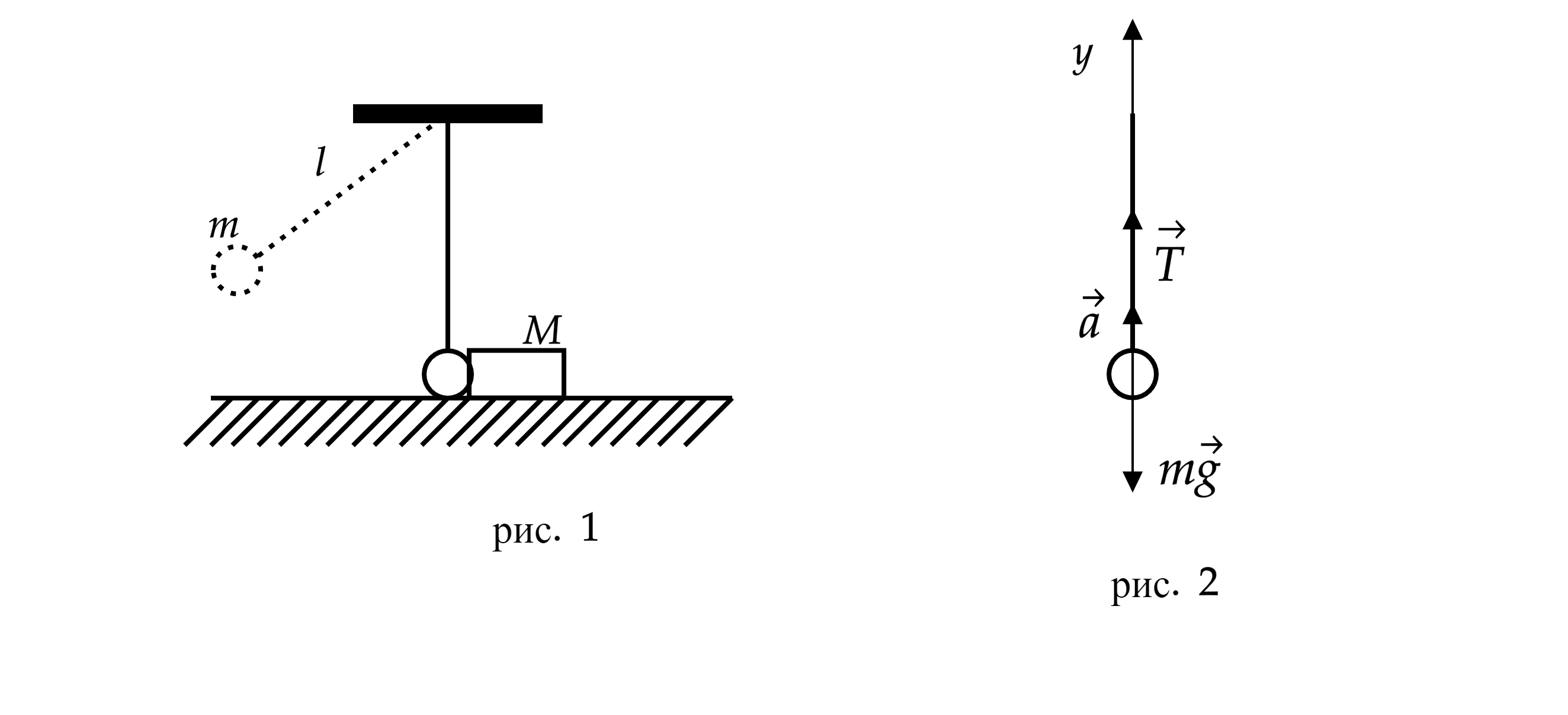
Запишем второй закон Ньютона в момент, когда шарик касается бруска.
где - полное ускорение.
В проекции на вертикальную ось, направленную вверх
где – сила тяжести,
– центростремительное ускорение,
– скорость шарика.
Распишем все составляющие закона по формулам и получим:
– скорость перед столкновением с бруском. Также запишем закон сохранения импульса при абсолютно неупругом
ударе
где – импульс шарика,
– импульс бруска,
– импульс бруска и шарика после удара. Распишем все составляющие по
формулам, с учетом того, что брусок покоится
Выразим скорость перед столкновением:
Подставим выраженную скорость в закон, который мы расписали выше:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




