.04 Законы сохранения в механике
Ошибка.
Попробуйте повторить позже
По гладкой наклонной плоскости, составляющей угол с горизонтом, скользит из состояния покоя брусок массой
В тот момент, когда брусок прошёл по наклонной плоскости расстояние
в него попала и застряла в нём
летящая навстречу ему вдоль наклонной плоскости пуля массой
После попадания пули брусок поднялся вверх вдоль
наклонной плоскости на расстояние
от места удара. Найдите скорость пули перед попаданием в брусок. Трение бруска о
плоскость не учитывать.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Брусок движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать брусок моделью материальной точки.
3. Процесс попадания пули мгновенный, значит, действием внешних сил можно пренебречь, можно применить закон сохранения импульса. Так как размеры пули меньше размера бруска, то ее также можно описывать моделью материальной точки.
Решение
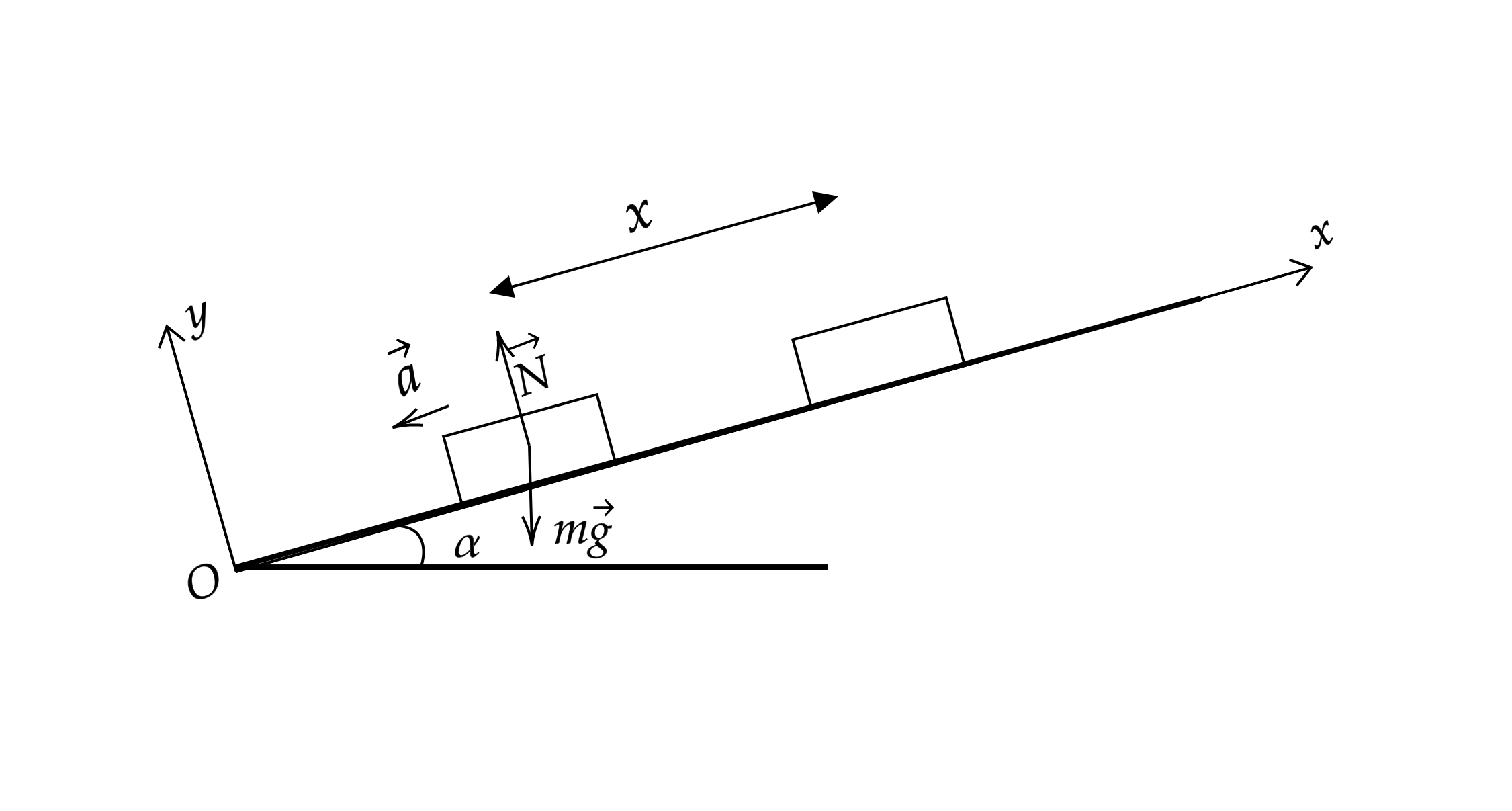
Запишем второй закон Ньютона
Здесь – сила реакции опоры,
– ускорение тела.
Спроецируем второй закон Ньютона на ось
Тело будет двигаться по наклонной поверхности с ускорением . У нас имеется формула расстояния
где и
– конечная и начальная скорости тела,
– ускорение тела.
В нашем случае тело двигается из состояния покоя, то есть
Отсюда конечная скорость равна
Воспользуемся законом сохранения импульса
Или в проекции на ось, совпадающую с движением тела
где – скорость составного тела сразу после попадания пули.
Дальше воспользуемся первоначальным уравнением расстояния, с учетом того, что ускорение , а конечная скорость
равна 0
Выразим
Подставим (1) и (2) в закон сохранения импульса:
Выразим нужную нам скорость:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




