.05 Статика
Ошибка.
Попробуйте повторить позже
Два небольших массивных шара массами кг и
кг закреплены на концах невесомого стержня
, лежащего
горизонтально на опорах
и
. Длина стержня AB
м, а расстояние AC равно 0,2 м. Сила давления стержня на опору D в
2 раза больше, чем на опору C. Каково расстояние между опорами CD? Сделайте рисунок с указанием внешних сил, действующих на
систему тел «стрежень и шары».
Обоснуйте применимость законов, используемых для решения задачи.

Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной
(ИСО).
2. Описываем стержень с шарами моделью абсолютно твёрдого тела (форма и размеры тела неизменны, расстояние между любыми
двумя точками тела остаётся неизменным).
3. Стержень не движется поступательно, поэтому векторная сумма сил, действующих на него, равна нулю.
4. Стержень не вращается, поэтому сумма моментов сил относительно оси, проходящих через точку А перпендикулярно плоскости
рисунка, равна нулю.
5. Согласно третьему закону Ньютона силы, с которыми шары и стержень взаимодействуют друг с другом, равны по модулю и
направлены в противоположные стороны.
Решение
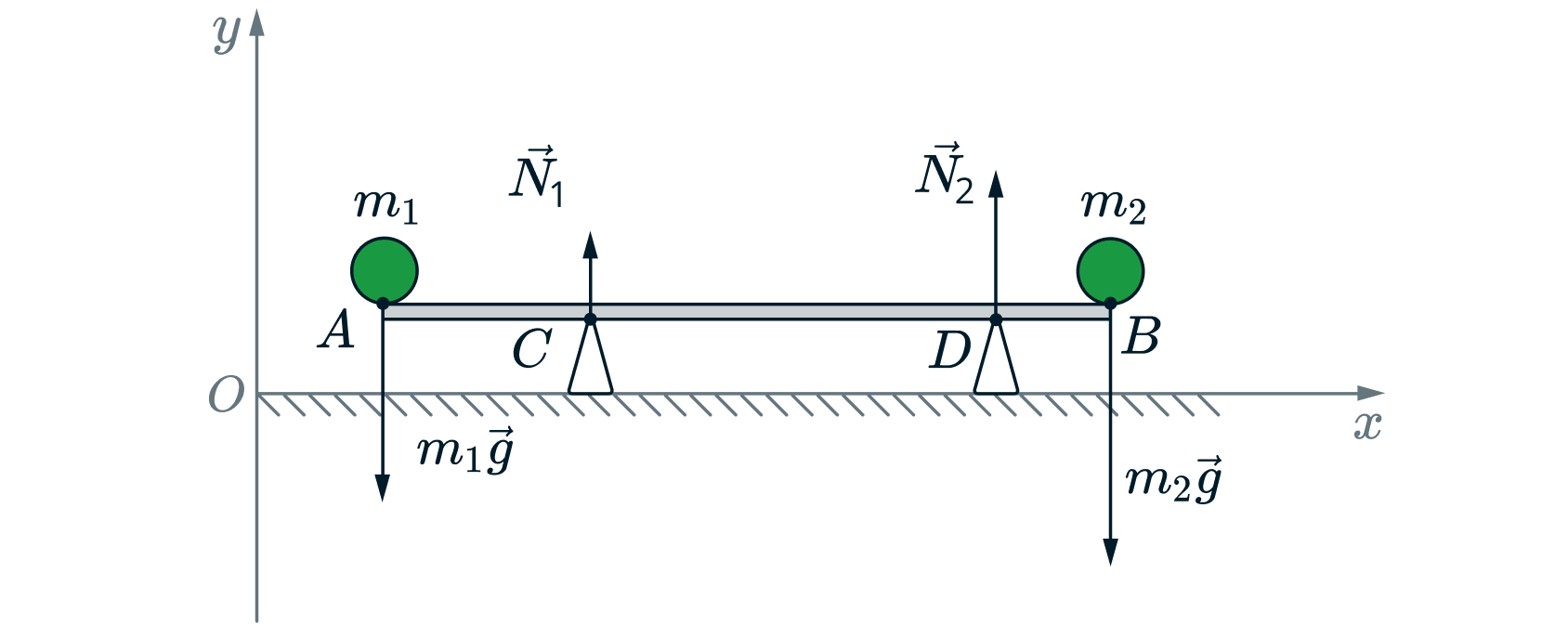
На твердое тело, образованное стержнем и двумя шарами, действуют силы тяжести и
, приложенные к центрам шаров, и
силы реакции опор
и
. По третьему закону Ньютона модули сил реакции равны соответствующим модулям сил давления
стержня на опоры, поэтому
(в соответствии с условием задачи).
Момент силы можно найти по формуле: , где
- сила, а
- её плечо до рассматриваемой оси вращения.
В инерциальной системе отсчёта Oxy, связанной с Землёй, условия равновесия тела приводят к системе уравнений (второй закон
Ньютона и правило моментов относительно точки А):
|
|
где ,
– плечо силы
.
Так как , то систему уравнений можно переписать в виде
|
|
Поделим второе уравнение на первое
Отсюда
| Критерии оценивания выполнения задачи | Баллы |
| Критерий 1 | |
| Верно обоснована возможность испольования законов | 1 |
| (закономерностей). В данном случае: выбор ИСО, модель материальной точки, модель абсолютно твёрдого тела, применение второго закона Ньютона, правила моментов | |
| В обосновании возможности использования законов | 0 |
| (закономерностей) допущена ошибка | |
|
ИЛИ
| |
| Обоснование отсутствует | |
| Критерий 2 | |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае - условия равновесия твёрдого тела относительно поступательного и вращательного движений, второй закон Ньютона); | |
| II) описаны вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений величин, используемых | |
| в условии задачи, и стандартных обозначений величин, | |
| используемых при написании физических законов); | |
| III) проведены необходимые математические преобразования | |
| и расчёты (подстановка числовых данных в конечную формулу), | |
| приводящие к правильному числовому ответу (допускается решение | |
| «по частям» с промежуточными вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| фиизческой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| фиизческие законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков. | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И(ИЛИ)
| |
| В решении имеются лишние записы, не входящие в решение | |
| (возможно, неверные), которые не отделены от решения и не | |
| зачёркнуты | |
|
И(ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и(или) в математических преобразованиях/ | |
| вычислениях пропущены логически важные шаги. | |
|
И(ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка (в том числе | |
| в записи единиц измерений величины) | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| данной задачи, без каких-либо преобразований с их | |
| использованием, направленных на решение задачи. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения данной задачи (или утверждение, лежащее в основе | |
| решения), но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения данной | |
| задачи (или в утверждения, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




