.05 Статика
Ошибка.
Попробуйте повторить позже
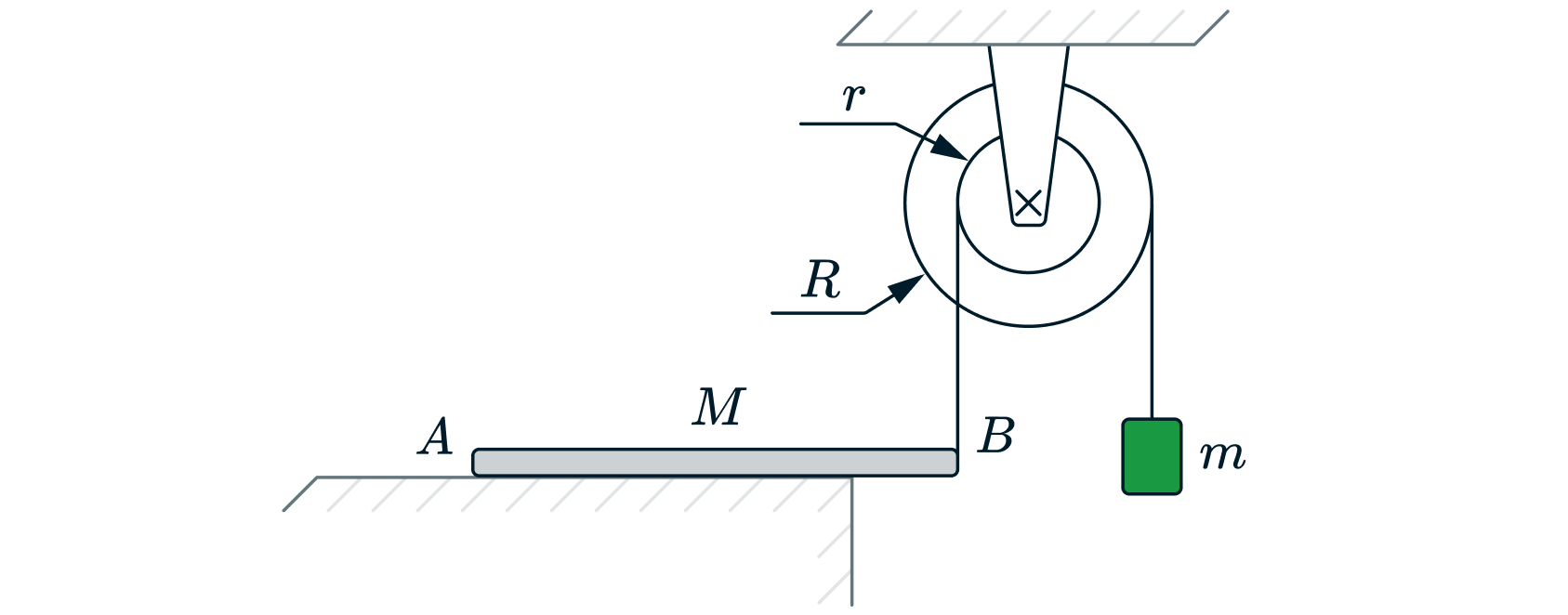
Однородный брусок массой
постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола,
свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой
конец нити закреплён на меньшем из двух дисков идеального составного блока. На большем диске этого блока закреплена другая
лёгкая нерастяжимая нить, на которой висит груз массой
Диски скреплены друг с другом, образуя единое целое.
Сделайте рисунок с указанием сил, действующих на брусок
блок и груз
Найдите минимальное
значение
при котором система тел остаётся неподвижной.
Обоснуйте применимость используемых законов к решению задачи.
Демоверсия 2023
Обоснование
1. Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО).
2. Брусок перед отрывом его правого края от поверхности стола будем считать твёрдым телом с осью вращения, проходящей
перпендикулярно плоскости рисунка через точку A. Условие равновесия относительно вращения твёрдого тела на оси – равенство
нулю суммы моментов сил, приложенных к телу, относительно этой оси. 3. Нити нерастяжимы, поэтому, если покоится брусок, то
покоятся и все остальные тела системы.
4. Нити лёгкие, поэтому величина силы натяжения каждой нити в любой её точке одна и та же. В том числе: ,
(см.
рисунок в решении).
5. Блок идеальный (трения в осях нет, масса блока пренебрежимо мала). Поэтому условие равновесия блока – равенство нулю суммы
моментов сил натяжения нитей относительно оси блока.
6. Груз может двигаться только поступательно вдоль вертикальной оси Oy, лежащей в плоскости рисунка. Поэтому для груза
используем модель материальной точки и применим второй закон Ньютона. Вследствие этого условие равновесия – сумма
приложенных к грузу сил равна нулю.
Решение
Брусок начнёт отрываться от поверхности стола, когда сила реакции опоры со стороны стола станет равна нулю. Рассмотрим случай
минимальности груза. Брусок ещё покоится на столе, но касается стола только в точке A, тогда сила реакции опоры приложена в
точке и направлена вертикально вверх.
Расставим силы, действующие на брусок , блок и груз
.
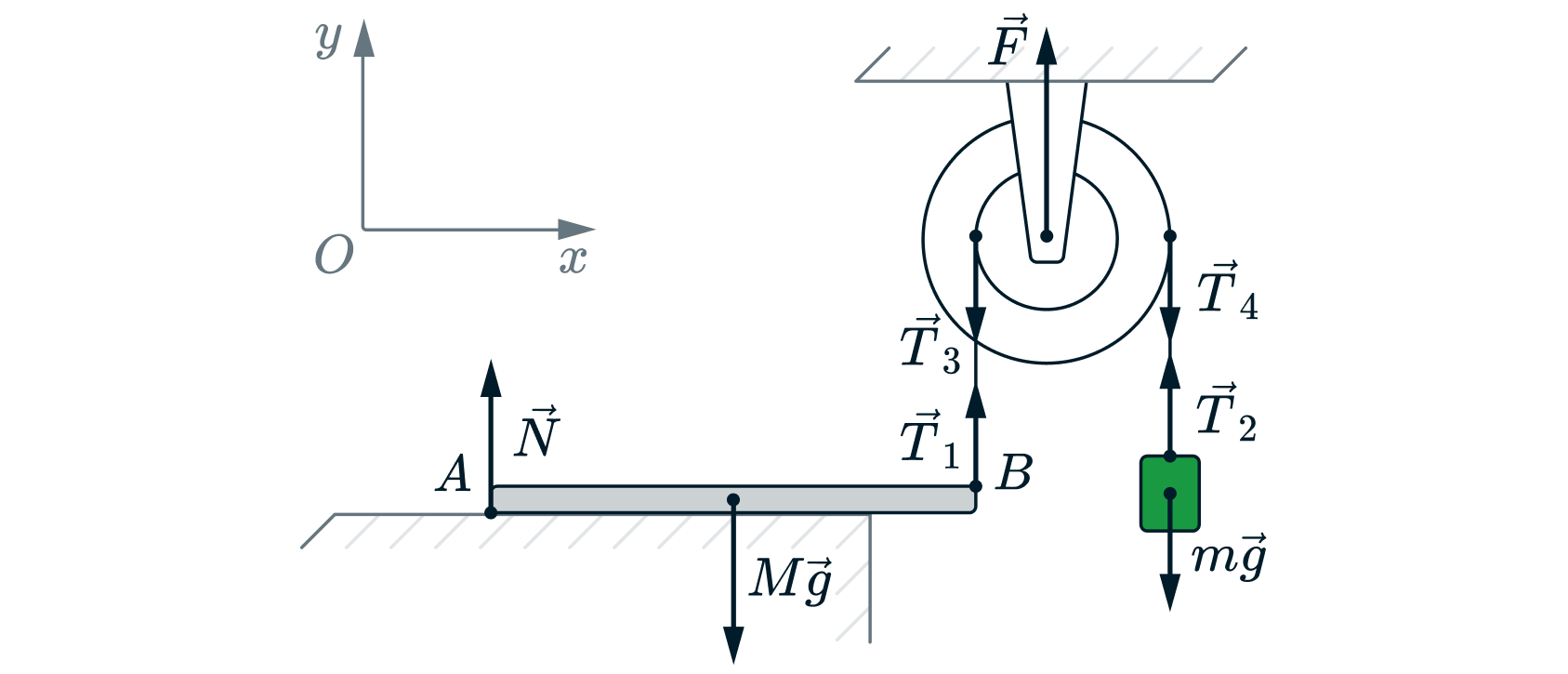
Запишем уравнение моментов относительно оси, проходящей перпендикулярно рисунку в точке :
Отсюда
Запишем второй закон Ньютона для груза
где – ускорение груза.
Так как система покоится, то . Спроецируем второй закон Ньютона на оси
:
Аналогично правило моментов для блока, относительно оси, проходящей через его центр:
Из условия лёгкости нити ,
, тогда
Подставим (1) и (2) в (3)
| Критерии оценивания выполнения задачи | Баллы |
| Критерий 1 | |
| Верно обоснована возможность испольования законов | 1 |
| (закономерностей). В данном случае: выбор инерциальной системы отсчёта, модель твёрдого тела, модель материальной точки, особенности применимости условий равновесия | |
| В обосновании возможности использования законов | 0 |
| (закономерностей) допущена ошибка | |
|
ИЛИ
| |
| Обоснование отсутствует | |
| Критерий 2 | |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае - уравнение моментов сил для двух тел, второй закон Ньютона); | |
| II) описаны вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений величин, используемых | |
| в условии задачи, и стандартных обозначений величин, | |
| используемых при написании физических законов); | |
| III) проведены необходимые математические преобразования | |
| и расчёты (подстановка числовых данных в конечную формулу), | |
| приводящие к правильному числовому ответу (допускается решение | |
| «по частям» с промежуточными вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| фиизческой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| фиизческие законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков. | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И(ИЛИ)
| |
| В решении имеются лишние записы, не входящие в решение | |
| (возможно, неверные), которые не отделены от решения и не | |
| зачёркнуты | |
|
И(ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и(или) в математических преобразованиях/ | |
| вычислениях пропущены логически важные шаги. | |
|
И(ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка (в том числе | |
| в записи единиц измерений величины) | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| данной задачи, без каких-либо преобразований с их | |
| использованием, направленных на решение задачи. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения данной задачи (или утверждение, лежащее в основе | |
| решения), но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения данной | |
| задачи (или в утверждения, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




