.05 Статика
Ошибка.
Попробуйте повторить позже
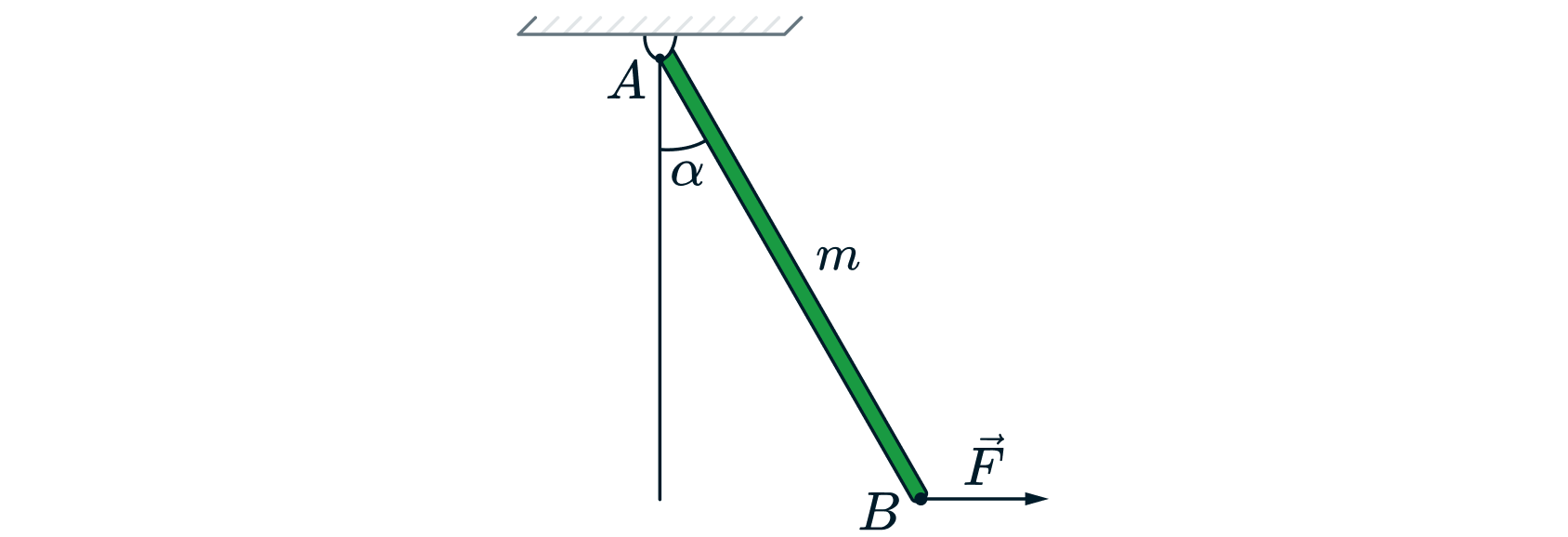
Однородный стержень постоянного поперечного сечения прикреплён верхним концом к шарниру, в котором он может без
трения поворачиваться в плоскости рисунка. Масса стержня
кг. Если к нижнему концу стержня приложена в
плоскости рисунка постоянная горизонтальная сила
, то в равновесии стержень образует с вертикалью угол
(
). Чему равен модуль силы, с которой стержень действует в равновесии на шарнир? Сделайте рисунок с
указанием сил, действующих на стержень
. Обоснуйте применимость используемых законов к решению задачи.
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Стержень будем описывать моделью абсолютно твердого тела - его форма и размеры неизменны, расстояние между
любыми двумя точками остаются неизменным. Так как стержень однородный, то его центр тяжести находится
посередине.
3. Движение абсолютно твердого тела можно описать совокопнустью движений - поступательного и вращательного. Поэтому для
равновесия твердого тела в ИСО необходимо два условия. Одно для поступательного движения, другое - для вращательного
движения.
4. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно
поступательного движения). Также применимо правило моментов (условие равновесия твёрдого тела относительно вращательного
движения)
Решение
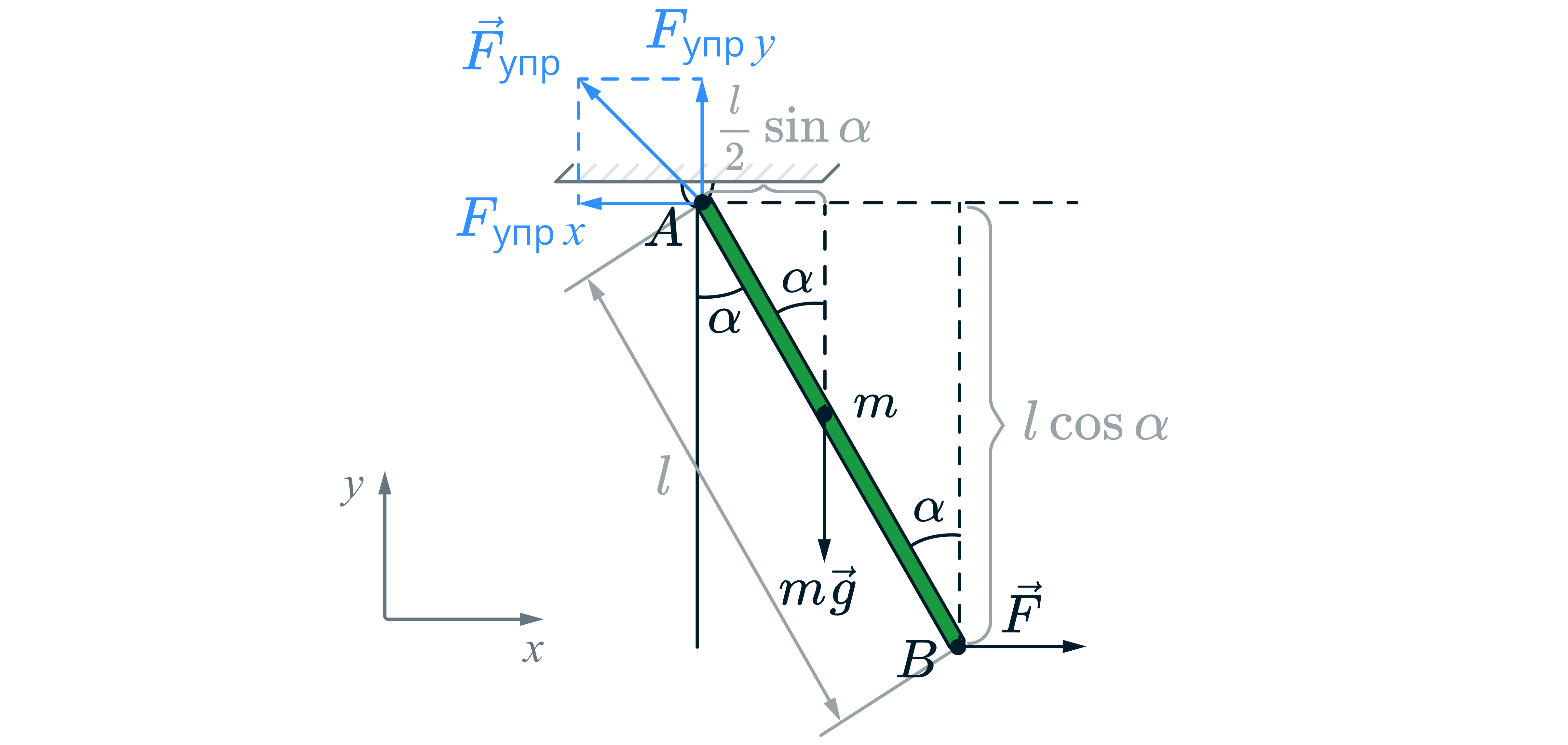
Запишем условие равновесия ( пункт 3) через второй закон Ньютона
Введем декартовую систему координат и запишем второй закон Ньютона в проекциях на оси
|
|
Тогда по правилу треугольника для векторов
Пусть длина стержня . Запишем второе условие равновесия через правило моментов. Рассмотрим моменты силы относительно
оси, проходящей через точку
.
Тогда
Тогда учитывая выражение для силы упругости, получим
По третьему закону Ньютона сила упругости равна силе, которая действует на шарнир со стороны стержня.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




