.05 Статика
Ошибка.
Попробуйте повторить позже
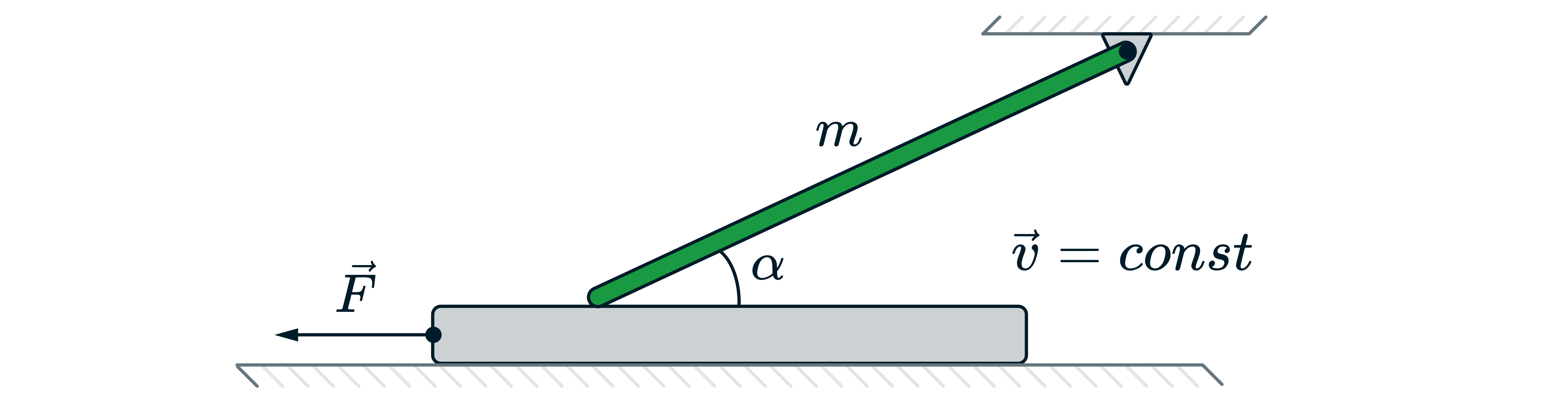
Однородный тонкий стержень массой одним концом шарнирно прикреплён к потолку, а другим концом опирается на массивную
горизонтальную доску, образуя с ней угол
. Под действием горизонтальной силы
доска движется поступательно влево с
постоянной скоростью (см. рисунок). Стержень при этом неподвижен. Найдите
, если коэффициент трения стержня по доске
= 0,2, а сила
= 0,9 Н. Трением доски по опоре и трением в шарнире пренебречь. Обоснуйте применимость законов, используемых
для решения задачи.
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной
(ИСО).
2. Описываем стержень моделью твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела
остаётся неизменным).
3. Сумма приложенных к стержню внешних сил равна нулю, так как он находится в равновесии относительно поступательного
движения. Сумма моментов этих сил относительно оси, проходящей перпендикулярно плоскости рисунка через точку шарнирного
крепления (точку О), равна нулю, так как стержень не вращается.
4. Доска движется поступательно. Движение доски в ИСО можно описать с помощью законов Ньютона, сформулированных для
материальных точек.
5. Согласно третьему закону Ньютона силы, с которыми доска и стержень взаимодействуют друг с другом, равны по модулю и
направлены в противоположные стороны.
Решение
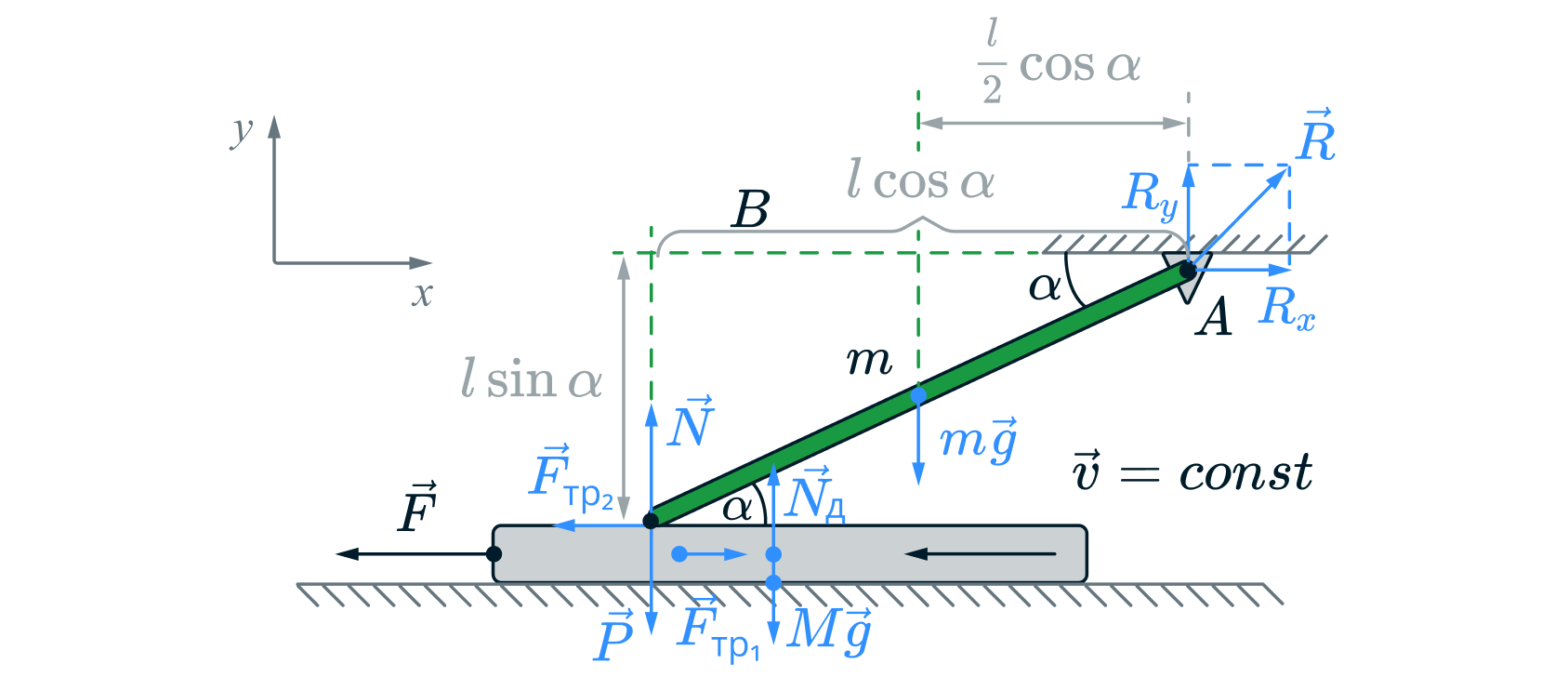
Т.к. доска движется равномерно, то по второму закону Ньютона в проекции
Т.к. стержень находится в равновесии, то запишем правило моментов относительно оси
По закону Амонтона-Кулона
По третьему закону Ньютона
Тогда выражая из правила моментов и учитывая, что
Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




