.05 Статика
Ошибка.
Попробуйте повторить позже
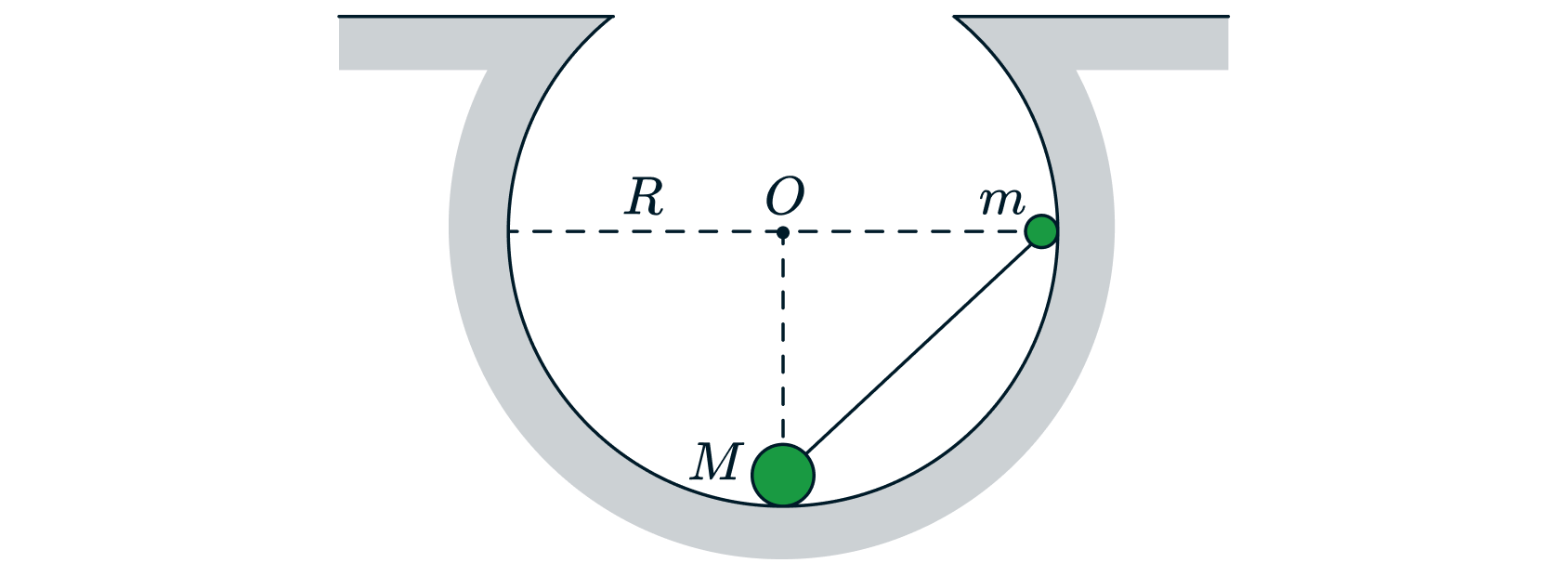
Маленькие шарики, имеющие массы и
г, соединены друг с другом стержнем пренебрежимо малой массы. Полученная
гантель помещена в неподвижную сферическую выемку радиусом
так, что шарик
находится в нижней точке выемки, а
шарик
касается стенки выемки на высоте
от этой точки (см. рисунок). Коэффициент трения между шариком
и дном
выемки
, трение между шариком
и стенкой выемки отсутствует. При каких значениях
гантель покоится в
показанном на рисунке положении? Сделайте рисунок с указанием внешних сил, действующих на гантель. Обоснуйте применимость
законов, используемых для решения задачи.
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Размерами шариков можно пренебречь, поэтому их можно считать материальными точками.
3. Стержень+гантели будем описывать моделью абсолютно твердого тела - его форма и размеры неизменны, расстояние между
любыми двумя точками остаются неизменным. Так как стержень жесткий и легкий, то силы натяжения, действующие на каждый
шарик, будут равны по модулю.
4. Движение абсолютно твердого тела можно описать совокопнустью движений - поступательного и вращательного. Поэтому для
равновесия твердого тела в ИСО необходимо два условия. Одно для поступательного движения, другое - для вращательного
движения.
5. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно
поступательного движения). Также применимо правило моментов (условие равновесия твёрдого тела относительно вращательного
движения)
Решение
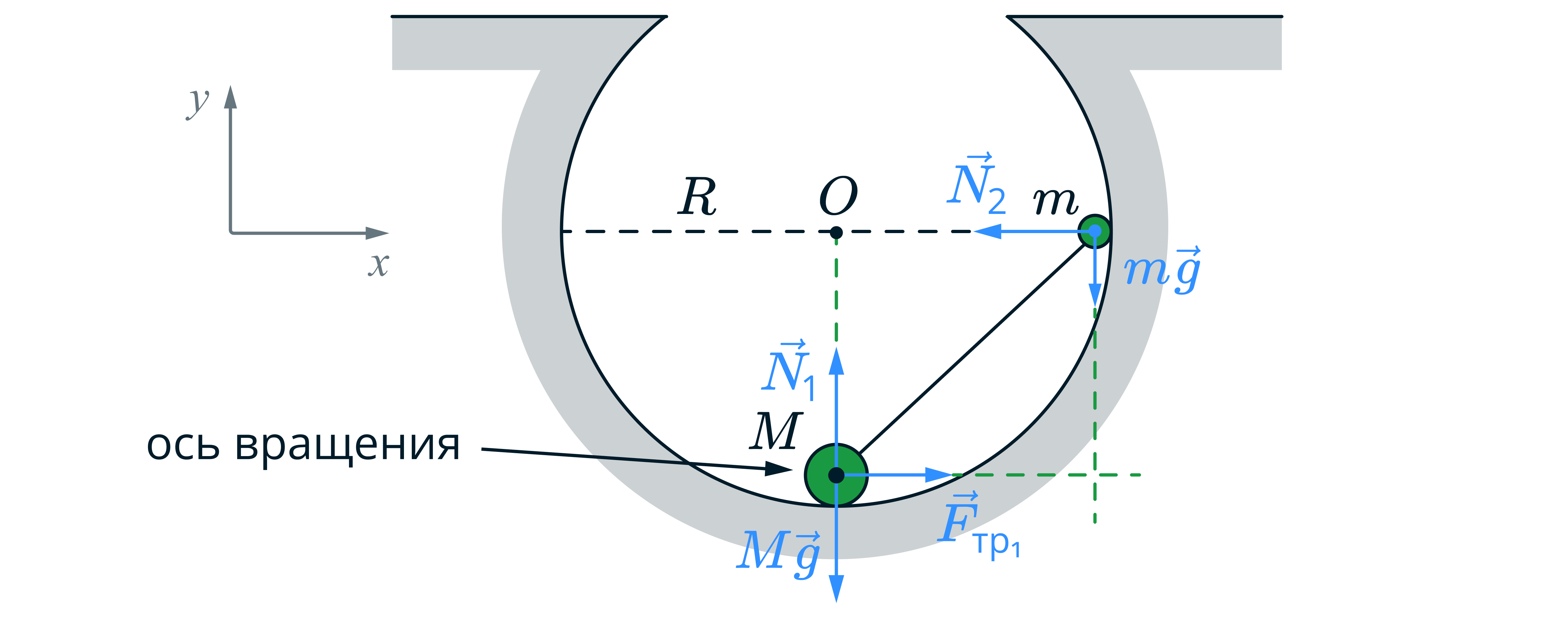
Запишем условие равновесия (пункт 3) через второй закон Ньютона
Введем декартовую систему координат и запишем второй закон Ньютона в проекциях на оси
|
|
Запишем условие равновесия через правило моментов относительно оси вращения. Тогда
Т.к. сила трения пока есть
Тогда получаем, что
Тогда гантель покоится при
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




