14.11 Построение сечений
Ошибка.
Попробуйте повторить позже
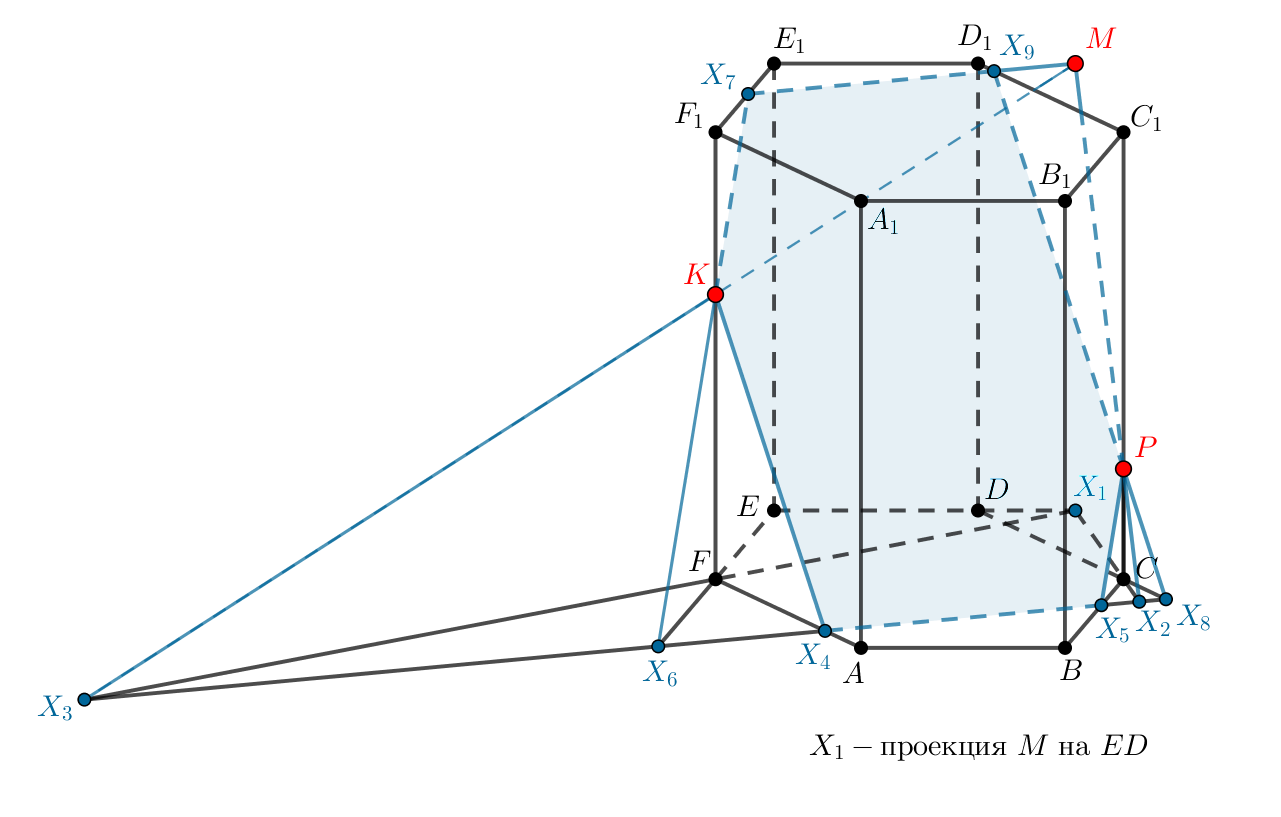
Постройте сечение правильной шестиугольной призмы плоскостью, проходящей
через точки
и
(точка
лежит в плоскости грани
на
продолжении
за точку
).

Назовем плоскость плоскостью
Пусть — ортогональная проекция точки
на плоскость
Тогда
пересекает
в точке
в которой прямая
пересекает прямую
(так как
— проекция точки
на плоскость
). Плоскость
также пересекает
в точке
в которой прямая
пересекает
прямую
(так как
— проекция точки
на плоскость
). Таким
образом,
пересекает
по прямой
Пусть
тогда
— сторона сечения
призмы плоскостью
Пусть Тогда
— точка, лежащая в
следовательно,
— еще одна сторона сечения, где
Пусть Тогда
— точка, лежащая в
следовательно,
— еще одна сторона сечения, где
Получаем еще одну сторону сечения Тогда сечение призмы плоскостью
— шестиугольник
могла пересечь не стороны
и
, а их продолжения (либо
продолжение только одной из этих сторон), тогда сечение получилось бы
другим.
могла бы пересечь не
а ребро
тогда сечение выглядело
бы по-другому.
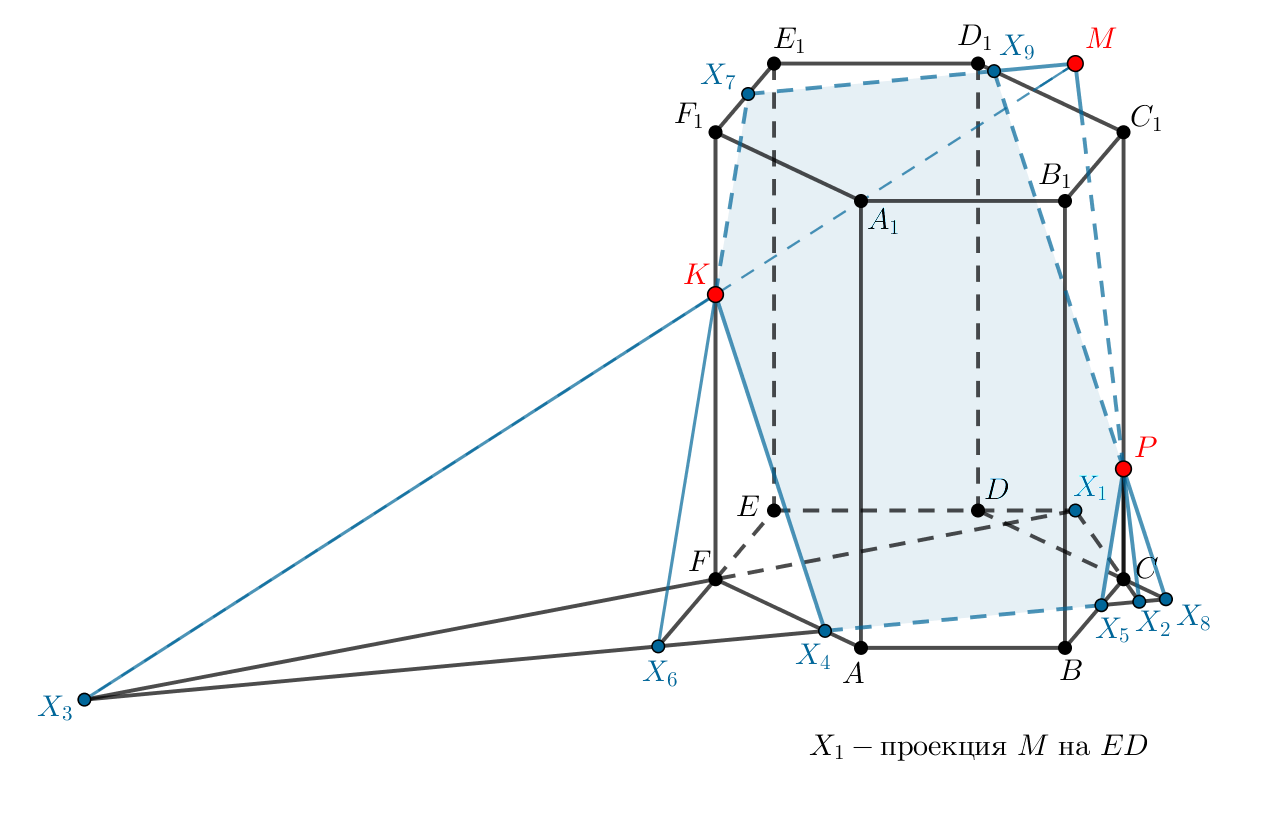
Заметим, что
в нашем случае пересечет именно ребро
так
как точка
лежит на ребре
следовательно, плоскость
пересекает
плоскость
по прямой
которая пересекает в результате
положения
отрезок
а не его продолжение.
Все зависит от положения точек
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




