19.17 Произвольные последовательности чисел
Ошибка.
Попробуйте повторить позже
По кругу выписаны несколько целых чисел, причем каждое из чисел больше суммы двух предыдущих, если двигаться по часовой
стрелке. Например, если выписаны три числа
и
(нумерация по часовой стрелке), то должны выполняться три
неравенства:
и
а) Может ли количество чисел равняться 10?
б) Могут ли два неотрицательных числа стоять рядом, если выписано не менее 4 чисел?
в) Какое наименьшее количество отрицательных чисел могло быть выписано, если всего чисел 100?
а) Да, может, например, так:
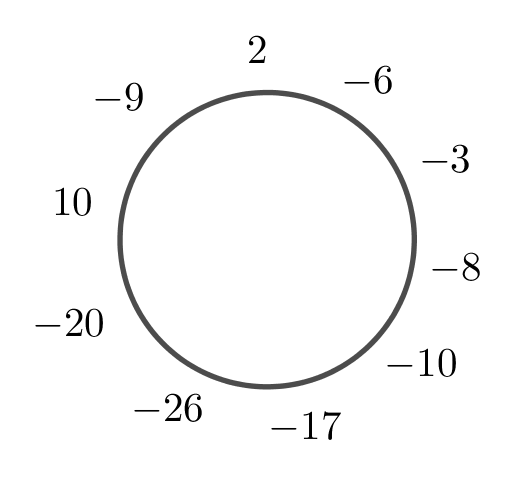
б) Обозначим через общее количество чисел в круге. Пусть, не умаляя общности,
и
— два соседних
неотрицательных числа. Следующее за ними по часовой стрелке число
по условию должно быть больше суммы
а
значит, больше каждого из
и
Будем двигаться далее по часовой стрелке, проводя аналогичное рассуждение (нам ничто
не помешает, так как
и
снова неотрицательные). Получим, что при движении по часовой стрелке начиная с
числа
строго увеличиваются, причем
и
следовательно,
Однако по условию
должно быть больше
суммы
что невозможно при
и неотрицательном
Значит, два неотрицательных числа не могли стоять
рядом.
в) В предыдущем пункте мы доказали, что неотрицательные числа не могут соседствовать в круге, следовательно, отрицательных чисел должно быть не меньше половины от общего количества, то есть не меньше 50.
Допустим отрицательных ровно 50, тогда неотрицательных тоже 50, и они должны чередоваться в круге. Обозначим числа
по часовой стрелке, не умаляя общности, будем считать, что
отрицательное. Тогда из чередования мы знаем, что
неотрицательное. По условию должно выполняться
следовательно,
— отрицательное число, большее, чем
Аналогично получаем (нам ничто не помешает, так как важна только отрицательность/неотрицательность числа, а она при
сдвиге на 2 по часовой стрелке сохраняется), что
а также
Получаем противоречивую цепочку
неравенств
|
|
Значит, 50 отрицательных быть не могло. На 51 отрицательное число строится следующий пример:

а) Да
б) Нет
в) 51
| Содержание критерия | Балл |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующий результатов: — пример в пункте а); — обоснованное решение в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




