18.22 Графика. Окружность

1) Изобразим график первого уравнения.

а) При уравнение принимает вид:

Мы получили уравнение окружности (назовем ее ) с центром в точке и радиусом 2.

б) При уравнение принимает вид:

Таким образом, мы получили верное равенство. Следовательно, мы получили множество точек, абсцисса которых равна нулю.

в) При уравнение принимает вид:

Мы получили уравнение окружности (назовем ее ) с центром в точке и радиусом 4.

2) Уравнение задает множество прямых, параллельных прямой То есть это прямые, угол наклона которых к положительному направлению оси равен

Таким образом, получаем следующую картинку, на которой голубым цветом изображен график первого уравнения:

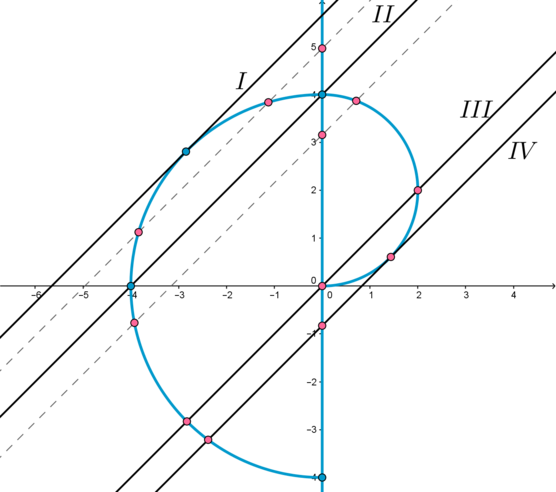
3) Для того, чтобы система имела 3 решения, нужно, чтобы при некотором фиксированном прямая пересекала «голубой график» ровно в трех точках.

Таким образом, нам подходят следующие случаи:

– когда прямая находится между положениями и (не включая эти случаи). Случай — касание прямой и окружности Случай — прохождение прямой через точку пересечения окружности и прямой

– когда прямая находится между положениями и (не включая и включая ). Случай — прохождение прямой через точку пересечения окружности и прямой

– когда прямая находится в положении — касается окружности

Рассмотрим каждый из этих случаев по отдельности.

Между и

Найдем значение при котором прямая находится в положении В этом случае

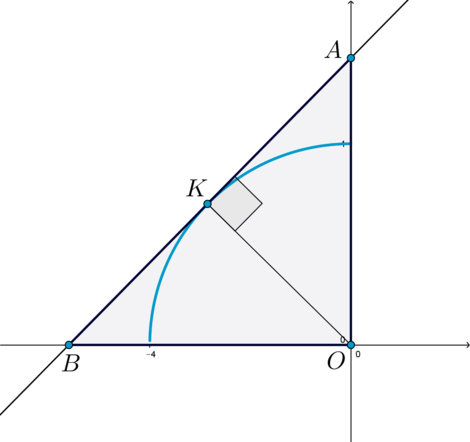
Пусть — точки пересечения прямой с осями координат, — точка касания. Тогда как радиус, проведенный в точку касания. Длина прямоугольный. Тогда и получаем

Найдем значение при котором прямая находится в положении В этом случае она проходит через точку следовательно,

Таким образом, нам подходят значения

Между и

Найдем при котором прямая находится в положении В этом случае она проходит через точку то есть

Таким образом, нам подходят

Положение

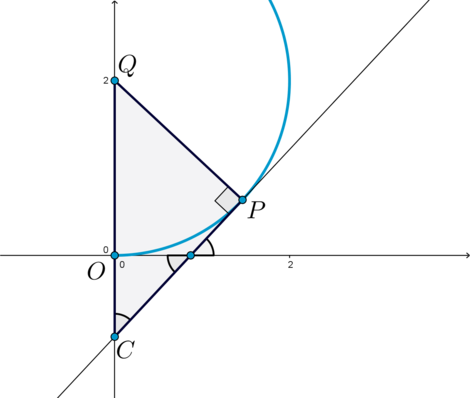
В этом случае Пусть — центр окружности — точка касания, — точка пересечения с осью ординат. Тогда — прямоугольный.

Ранее мы говорили, что прямая наклонена к положительному направлению оси под углом откуда будет следовать, что и Радиус отрезок так как Следовательно,

Таким образом, объединяя все случаи, получаем