18.22 Графика. Окружность

Оба уравнения системы при задают окружности: первое уравнение – окружность с центром в точке и радиуса ; второе – окружность с центром в точке и радиуса .
При второе уравнение задает точку , которая не является решением первого уравнения. Следовательно, при система не имеет решений, значит, – не подходит.

 

Рассмотрим случай, когда .
Система будет иметь единственное решение, когда окружности будут касаться друг друга (внутренним или внешним образом). Заметим, что центры обеих окружностей находятся на прямой . То есть линия центров окружностей параллельна оси абсцисс.

 

1) Пусть окружности касаются внешним образом в точке . Это одна из двух картинок:
 

 

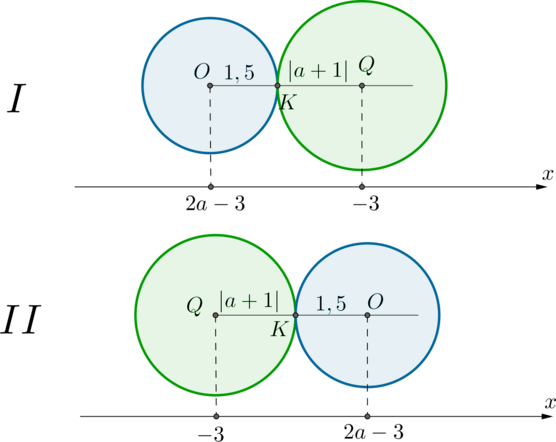
Заметим, что, с одной стороны, расстояние между центрами окружностей равно сумме радиусов: , а с другой стороны, равно . Получаем уравнение:

2) Пусть окружности касаются внутренним образом в точке . Это также одна из двух картинок (а также симметричные картинки, то есть когда точка касания находится слева):
 

 
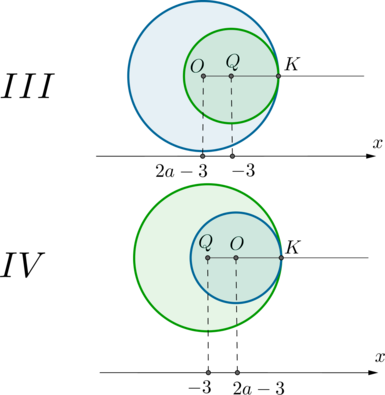
В этих случаях длина отрезка , с одной стороны, равна , а с другой стороны, она равна разности радиусов: (ставим модуль, потому что неизвестно, какой радиус больше, то есть как окружность с центром может быть вписана в окружность с центром , так и наоборот). Получаем уравнение:

Таким образом, окончательный ответ: