18.23 Графика. Окружность
Ошибка.
Попробуйте повторить позже
Найдите все значения при каждом из которых система уравнений
имеет ровно одно решение.
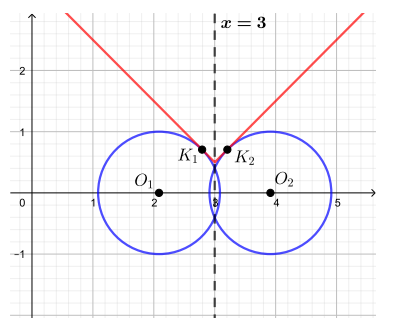
Рассмотрим первое уравнение. Оно задает окружность в системе координат с
центром в точке
и радиусом 1. Другими словами, это семейство
окружностей с радиусом 1 и центром в произвольной точке прямой
(то есть
оси абсцисс).
Второе уравнение задает «уголок» модуля с ветвями вверх и вершиной в точке
Левая ветвь содержится в прямой
правая — в прямой
Построим графики.
![]()
Заметим, что если окружность с центром в точке нам подходит
(то есть имеет ровно одну точку пересечения с уголком), то и окружность,
симметричная ей относительно прямой
(эта прямая — ось симметрии
уголка) с центром в точке
нам тоже подойдет. Более
того, очевидно, что никакие другие окружности не подойдут. Осталось понять, при
каких
(то есть центр не правее оси симметрии) окружность имеет ровно
одну точку пересечения с левой веткой уголка. Часть решения ниже, выделенная
курсивом, нужна исключительно для неформального понимания задачи, на
экзамене так писать не следует.
Представим нашу ситуацию следующим образом. У нас есть окружность
фиксированного радиуса, центр которой «скользит» по оси абсцисс. Давайте
двигать окружность из вправо до тех пор, пока она не «упрется» в
уголок (или, другими словами, пока не соприкоснется с уголком). В этот
момент окружность либо будет касаться (прямая будет касательной к
окружности) левой ветки уголка, либо «упираться» в точку — вершину уголка
(при этом прямая не будет являться касательной к окружности!).
![]()
![]()
Во втором случае момент касания с прямой происходит раньше, чем момент касания с уголком (и только при движении дальше вправо мы упираемся в вершину уголка), так как касание происходит в точке, принадлежащей продолжению прямой (пунктирная часть).
Найдем положение касания с окружности с прямой
содержащей левую ветвь уголка. Если точка касания окружности и прямой будет
лежать левее вершины уголка (т.е. координата точки касания по оси
не
больше, чем 3) — реализовалась первая ситуация, в противном случае
реализовалась вторая.
Радиус окружности равен единице, значит, в моменте касания центр
окружности лежит на расстоянии 1 от прямой Построим прямую
левее
параллельную
на расстоянии 1 от
Искомое положение окружности
возникает, когда центр окружности попадает в точку
пересечения прямой
и
оси абсцисс, по которой движется центр.
![]()
Пусть — точка пересечения
с осью абсцисс,
— точка касания
окружности и прямой
и равен расстоянию между прямыми — это 1
по построению.
так как коэффициент при
равен
Тогда в полученном равнобедренном прямоугольном треугольнике
и координата по
точки
равна
а координата по
точки касания равна
Легко проверить, что это меньше, чем 3 —
координата по
вершины уголка и оси симметрии, значит, реализована первая
ситуация (касание с левой веткой). Итого нам подходит
которому соответствует положение
центра, а также
которому соответствует симметричное относительно оси положение центра —
Таким образом,
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточно обоснованное построение | 3 |
| ИЛИ | |
| недостаточно обоснован какой-либо момент при исследовании | 3 |
| Верно рассмотрен один из двух случаев и
найдено одно из значений параметра | 2 |
| ИЛИ | |
| верно проанализированы оба случая, но в ходе решения значения параметров найдены неверно | |
| Задача верно сведена к исследованию графически, выполнено верное построение с обоснованием | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




