18.23 Графика. Окружность
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых система
имеет решения.
Преобразуем первое уравнение:
Оно задает окружность с центром в точке и радиусом
Найдем траекторию центра окружности:
Таким образом, первое уравнение исходной системы задает окружность с центром в произвольной точке прямой и
радиусом
Второе уравнение исходной системы — это прямая
Построим графики.

Нас интересуют значения при которых окружность имеет точки пересечения с прямой
значит, ключевыми
положениями на рисунке для нас будут касания окружности с этой прямой. Заметим, что прямая
и
прямая-траектория
перпендикулярны. Следовательно, окружность будет касаться прямой
только в том
случае, если ее центр находится на расстоянии, равном радиусу окружности, от точки пересечения прямых — начала координат.
Изобразим случаи касания на картинке, начало координат обозначим через
центры окружностей в случаях касания — через
и
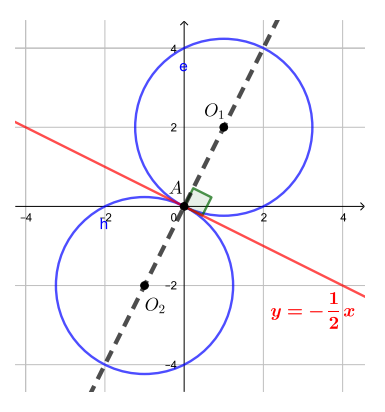
Мы поняли, что точки и
таковы, что
Очевидно также, что
и
Найдем
записав условие на расстояние между
и
Так как то получаем
Очевидно, что при любых
то есть когда центр принадлежит
отрезку
окружность будет иметь пересечения с прямой
а при любых
для которых
— не будет.
Получаем ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Верно найдены граничные
значения | 2 |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




